Một bài toán rất hay về bộ môn Bi-a (Billards)
Hãy giải bài toán dưới đây theo lời giải của trình độ của cấp tiểu học, trung học cơ sở và trung học phổ thông. Bạn có thể chọn bất cứ cấp bậc nào để giải, và có thể giải nhiều cấp bậc khác nhau.

Một bài toán rất hay về bộ môn Bi-a (Billards)
Hãy giải bài toán dưới đây theo lời giải của trình độ của cấp tiểu học, trung học cơ sở và trung học phổ thông. Bạn có thể chọn bất cứ cấp bậc nào để giải, và có thể giải nhiều cấp bậc khác nhau.

Bóng đánh từ A, chạm bàn tại N rồi bật ra rồi tiếp tục chạm-phản xạ từ các cạnh bàn với góc phản xạ bằng góc tới và sau 5 lần bóng phản xạ thì dừng lại ở góc D.

Do hình chữ nhật ABCD nhận KE nối 2 trung điểm của AD và BC làm trục đối xứng đồng thời điểm chạm khởi đầu A và điểm kết thúc D của bi-a là 2 điểm đối xứng nhau qua KE nên trong 5 điểm bi-a chạm bàn có 2 cặp điểm (M, N) và (P, Q) đối xứng nhau qua KE và điểm chạm còn lại chính là E trung điểm BC.
Từ đó suy ra các hình AMND, MNQP và PQCB là các hình chữ nhật với AM = DN = NQ = MP = 4, PB = QC = 2 và KA = KD = EB = EC = 3/2 (xem hình vẽ).
Sử dụng định lý Pitago ta có: AN = DM = NP = MQ = QE + PE = 5.
Vậy tổng chiều dài mà quả bóng đã đi từ A đến D là
AN + NP + PE + EQ + QM + MD = 25.
Theo em đáp án là 52(đơn vị độ dài ạ)
AB + BC + CD + DB + BC + CD = 2(AB + BC + CD) + DB = 2(10 + 3 + 10) + 3 = 52
Ta có thể giải bài Toán theo các cấp độ khác nhau:
- Cấp Tiểu học: Bóng Bi-a sẽ di chuyển đi và đập vào các cạnh của bàn Bi-a. Nếu bạn đếm số lần bóng đập vào các cạnh, bạn sẽ thấy rằng bóng đã đập vào các cạnh 5 lần trước khi dừng lại.
- Cấp Trung học cơ sở: Bóng Bi-a di chuyển theo hình dạng của một hình chữ nhật. Chiều dài của hình chữ nhật là 10 và chiều rộng là 3. Vì bóng di chuyển theo hình chữ nhật 5 lần trước khi dừng lại, tổng quãng đường mà bóng đã đi là 5 lần chu vi của hình chữ nhật. Chu vi của hình chữ nhật là (10 + 3) \(\cdot\) 2 = 26, vậy tổng quãng đường là 265 = 130.
- Cấp Trung học phổ thông: Bóng Bi-a di chuyển theo đường thẳng và phản xạ khi chạm vào các cạnh của bàn Bi-a. Điều này tạo ra một chuỗi các hình chữ nhật giống nhau. Mỗi hình chữ nhật có chiều dài là 10 và chiều rộng là 3. Vì bóng di chuyển qua 5 hình chữ nhật trước khi dừng lại, tổng quãng đường mà bóng đã đi là 5 lần chu vi của một hình chữ nhật. Chu vi của một hình chữ nhật được tính bằng công thức P = 2 \(\cdot\) (l + w), với l là chiều dài và w là chiều rộng. Thay số vào công thức, ta được P = 2 \(\cdot\) (10 + 3) = 26. Vậy tổng quãng đường là 26 \(\cdot\) 5 = 130.
.jpg)
Theo bạn, đáp án cho câu hỏi trong hình trên là gì?
Đáp án đúng là C. (0;1) ở đây ý chỉ tọa độ của (x;y) khi biểu diễn trên đồ thị chứ không phải một khoảng.
Đáp án là C vì
- Tại \(x=0;y=0;y'=0\)
- \(y'\) đổi dấu từ âm sang dương ở \(x\in(-\infty;2)\)
[CÒN 20 PHÚT ĐỂ THAM GIA TRÒ CHƠI TRẢ LỜI CÁC CÂU HỎI VỀ KIẾN THỨC TỔNG HỢP]
*Thể lệ, cơ cấu giải thưởng: các bạn có thể xem chi tiết tại " https://hoc24.vn/cau-hoi/tro-choi-tra-loi-cac-cau-hoi-ve-kien-thuc-tong-hop-gioi-thieu-xin-chao-cac-ban-minh-la-huynh-thanh-phong-la-mot-ctv-hom-nay-minh-se-to-chuc-ra-m.8826447584557 "
Cách tham gia:
+ Bước 1: vào quizizz.com/join
+ Bước 2: nhập mã 8455 1405
Hoặc sao chép sau đó dán bằng link sau: https://quizizz.com/join?gc=84551405
Kết thúc vào: 10 tháng 3 năm 2024
Cập nhật bảng xếp hạng như sau:
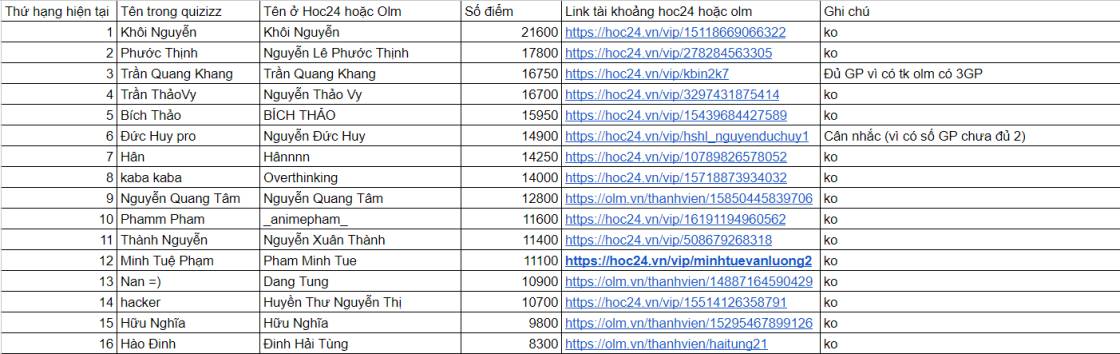
Nếu đã tham gia trò chơi mà chưa thấy tên trong bảng xếp hạng thì các bạn hay bình luận tên trong quizizz ngay bên dưới bài viết này nhé !
Bảng xếp hạng có thể được cập nhật tại:
https://docs.google.com/spreadsheets/d/1ViQjN0CMr7SIi1EjsmnRJ95EmkIUJcG6K8OVvIito1Q/edit#gid=0
Một quân mã cần di chuyển từ A đến B trên bàn cờ vua \(8\times8\). Chứng minh rằng với mọi vị trí tùy ý của A và B, luôn có cách để quân mã thực hiện hành trình với ít hơn hoặc bằng 6 bước.

Chơi cờ thoai cơ mà áp lực ngang zậy đó -)
Khi phát bài kiểm tra của một lớp, thầy giáo nói: “điểm trung bình của lớp chúng ta là 8.0”. Cả lớp reo hò.
“Nhưng điểm trung vị là 5”. Cả lớp không phản ứng gì vì chưa hiểu điều đó có nghĩa là gì.
Hỏi điều này có thể xảy ra không và từ các thông tin này có thể rút ra kết luận gì?
Nếu hệ điểm 10 thì điều này ko thể xảy ra, tư duy rất đơn giản, vì \(\dfrac{10+5}{2}< 8\)
Còn rút ra điều gì thì chắc là nhường mấy em học sinh lớp đó chứ thực sự mình cũng ko hiểu thông tin này cho biết điều gì. Vì trung bình có thể lớn hơn, nhỏ hơn hoặc bằng trung vị, tùy trường hợp.
Nếu thầy giáo nói điểm trung bình của lớp là 8.0, điều này có thể xảy ra nếu tổng số điểm của tất cả học sinh chia cho số lượng học sinh là 8. Điều này chỉ là điểm trung bình của toàn bộ lớp và có thể bị ảnh hưởng bởi các học sinh có điểm cao hoặc thấp.
Nếu điểm trung vị của lớp là 5, điều này có nghĩa là có một nửa số học sinh có điểm dưới 5 và một nửa có điểm trên 5. Điều này không nhất thiết phản ánh điểm trung bình của lớp.
Kết luận có thể rút ra từ thông tin này là lớp có sự biến động lớn trong điểm số, có thể có một số học sinh có điểm rất cao hoặc rất thấp, làm tăng giá trị của điểm trung bình. Đồng thời, điểm trung vị là 5 có thể là do một phần đáng kể của học sinh có điểm nằm trong khoảng 4 đến 6.
CÂU HỎI MÔN TOÁN 9 - CÂU HỎI ÔN THI VÀO 10 NĂM HỌC 2024 - 2025
----
Câu hỏi:
"Một hãng taxi công nghệ cao có giá cước (giá tiền khách hàng phải trả cho mỗi km) được tính theo các mức như sau:
Mức 1: Giá mở cửa cho 1km đầu tiên là 20000 đồng;
Mức 2: Từ trên 1km đến 25km;
Mức 3: Từ trên 25km;
Biết rằng anh A đi 32km phải trả tiền taxi là 479500 đồng còn chị B đi 41km phải trả 592000 đồng. Hỏi giá cước của hãng taxi trên ở mức 2 và mức 3 là bao nhiêu? Nếu khách hàng đi 24km thì phải trả taxi bao nhiêu tiền?"
Gọi giá cước của hãng Taxi ở mức 2 và mức 3 lần lượt là a(đồng) và b(đồng)
Số tiền anh A phải trả khi đi ở mức 2 là:
\(24\cdot a\left(đồng\right)\)
Độ dài quãng đường anh A đi ở mức 3 là:
32-25=7(km)
=>Số tiền anh A phải trả khi đi ở mức 3 là: 7b(đồng)
Độ dài quãng đường chị B đi ở mức 3 là:
41-25=16(km)
Số tiền chị B phải trả khi đi ở mức 2 là: 24a(đồng)
Số tiền chị B phải trả khi đi ở mức 3 là 16b(đồng)
Tổng số tiền anh A phải trả là 479500 đồng nên ta có phương trình:
20000+24a+7b=479500
=>24a+7b=459500(1)
Tổng số tiền chị B phải trả là 592000 đồng nên ta có phương trình:
20000+24a+16b=592000
=>24a+16b=572000(2)
Từ (1),(2) ta có hệ phương trình:
\(\left\{{}\begin{matrix}24a+16b=572000\\24a+7b=459500\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}9b=112500\\24a+16b=572000\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}b=12500\\3a+2b=71500\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}b=12500\\3a=71500-2\cdot b=71500-25000=46500\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}b=12500\\a=15500\end{matrix}\right.\left(nhận\right)\)
Vậy: Giá cước của hãng Taxi ở mức 2 và mức 3 lần lượt là 15500 đồng và 12500 đồng
Khi khách hàng đi 24km thì độ dài quãng đường khách hàng đi ở mức 2 là:
24-1=23(km)
Số tiền khách hàng phải trả khi đi 24km là:
\(23\cdot15500+20000=376500\left(đồng\right)\)
Bữa nay có chuyên mục ôn thi vào 10 + chuyên à a, cho em join với ạ :v
Gọi giá cước của hãng Taxi ở mức 2 và mức 3 lần lượt là a(đồng) và b(đồng) Số tiền anh A phải trả khi đi ở mức 2 là: 24 ⋅ a ( đ ồ n g ) Độ dài quãng đường anh A đi ở mức 3 là: 32-25=7(km) =>Số tiền anh A phải trả khi đi ở mức 3 là: 7b(đồng) Độ dài quãng đường chị B đi ở mức 3 là: 41-25=16(km) Số tiền chị B phải trả khi đi ở mức 2 là: 24a(đồng) Số tiền chị B phải trả khi đi ở mức 3 là 16b(đồng) Tổng số tiền anh A phải trả là 479500 đồng nên ta có phương trình: 20000+24a+7b=479500 =>24a+7b=459500(1) Tổng số tiền chị B phải trả là 592000 đồng nên ta có phương trình: 20000+24a+16b=592000 =>24a+16b=572000(2) Từ (1),(2) ta có hệ phương trình: { 24 a + 16 b = 572000 24 a + 7 b = 459500 => { 9 b = 112500 24 a + 16 b = 572000 ⇔ { b = 12500 3 a + 2 b = 71500 => { b = 12500 3 a = 71500 − 2 ⋅ b = 71500 − 25000 = 46500 => { b = 12500 a = 15500 ( n h ậ n ) Vậy: Giá cước của hãng Taxi ở mức 2 và mức 3 lần lượt là 15500 đồng và 12500 đồng Khi khách hàng đi 24km thì độ dài quãng đường khách hàng đi ở mức 2 là: 24-1=23(km) Số tiền khách hàng phải trả khi đi 24km là: 23 ⋅ 15500 + 20000 = 376500 ( đ ồ n g )
LÀM ONLINE ĐỀ MINH HỌA TỐT NGHIỆP NĂM 2025
(Kiến thức với chương trình lớp 10)
Kỳ thi tốt nghiệp trung học phổ thông 2025 gồm hai môn bắt buộc là Toán và Ngữ văn. Ngoài ra thí sinh được chọn hai môn trong các môn còn lại trong chương trình phổ thông, gồm: Hóa học, Vật lý, Sinh học, Ngữ văn, Địa lý, Lịch sử, Giáo dục Kinh tế và Pháp luật, Tin học, Công nghệ và Ngoại ngữ.
Bộ Giáo dục và Đào tạo cho biết đề thi được thiết kế theo hướng đánh giá năng lực phù hợp với chương trình giáo dục phổ thông 2018 và được thể hiện thông qua đề minh họa, bảng năng lực - cấp độ tư duy kèm theo. Thời điểm này, chương trình 2018 mới triển khai tới lớp 11. Do vậy các nội dung kiến thức được sử dụng trong các đề minh họa chủ yếu thuộc lớp 10 và 11. Bộ cho biết thêm các câu hỏi trong đề "cố gắng gắn với các bối cảnh có ý nghĩa", tức có tác dụng, giá trị nhất định đến đời sống, thực tiễn khoa học.
Trong phương án tổ chức thi tốt nghiệp THPT năm 2025, môn Ngữ văn được tổ chức thi theo hình thức tự luận trên giấy, các môn học khác được thi theo hình thức trắc nghiệm khách quan trên giấy. Thời gian làm bài thi môn Ngữ văn là 120 phút, Toán 90 phút, các môn học khác 50 phút.
Làm đề thi tại đây: https://dgnl.olm.vn/exam/de-minh-hoa-cac-mon-thi-tot-nghiep-thpt-nam-2025.2297421142
em xin trân thành cảm ơn thầy nhiều ạ

OLM CUNG CẤP BỘ ĐỀ KIỂM TRA CUỐI KÌ I
📚 Quý phụ huynh thân mến! Kỳ thi cuối học kỳ I đang đến gần, nhằm giúp các con ôn luyện tốt nhất, OLM đã biên soạn “𝐁𝐨̣̂ đ𝐞̂̀ 𝐤𝐢𝐞̂̉𝐦 𝐭𝐫𝐚 𝐜𝐮𝐨̂́𝐢 𝐤𝐢̀ 𝐈 các bộ môn”.
👉 Đề kiểm tra bám sát yêu cầu cần đạt của Chương trình học; đánh giá các kiến thức, kỹ năng quan trọng mà học sinh được học trong suốt học kì I.
👉 Mỗi bộ gồm đầy đủ: đề, đáp án và hướng dẫn chi tiết. Học sinh làm bài kiểm tra sẽ nhận được kết quả và nhận xét nhằm phát hiện các lỗ hổng kiến thức để tập trung ôn luyện hiệu quả.
📌 Truy cập link đề thi tại: https://olm.vn/tin-tuc/649320883
📲 Nhân dịp này, OLM cũng triển khai “CHƯƠNG TRÌNH KHUYẾN MẠI CUỐI KÌ I". Các tài khoản đăng kí mới hoặc gia hạn gói VIP sẽ được hưởng ưu đãi như sau:
+ Mua gói VIP 2 năm - TẶNG THÊM 6 tháng
+ Mua gói VIP 1 năm - TẶNG THÊM 3 tháng
+ Mua gói VIP 6 tháng - TẶNG THÊM 1 tháng
+ Mua gói VIP 1 tháng - TẶNG THÊM 7 ngày
* Thời gian khuyến mại từ: 12/12 - 31/12/2023.
👏 OLM trân trọng cảm ơn Quý Phụ huynh. Nếu cần cung cấp thêm thông tin, phụ huynh hãy liên hệ với đội ngũ của OLM để được hỗ trợ nhanh nhất !
-------------------------
Hệ thống Giáo dục Trực tuyến OLM
Hotline 24/7: 089 898 76 72 / 098 655 75 25
Email: a@olm.vn
Website: https://olm.vn
TỐI NAY DIỄN RA SỰ KIỆN PHỤ CUỐI CÙNG - VCET WINTER'23, MÙA 9
.png)
- Giải đấu Blitz không biến thể 3+0, diễn ra trong 100 phút, từ 19h45 Chủ Nhật (10/12):
lichess.org/tournament/ww3DIaMw
Cách thức đăng kí: không cần đăng kí, chỉ cần có tài khoản Lichess và gia nhập tổ chức tại: https://lichess.org/team/vietnam-chess-extended-tournament-vcet
CÒN 1 GIỜ DIỄN RA GIẢI CỜ VUA VCET WINTER'23 - MÙA 9
.png)
1 sự kiện lớn, 7 giải đấu, hơn 100 giải thưởng được trao ra và tổng giá trị giải thưởng lên tới hơn 20 triệu đồng. Giải đấu đầu tiên sẽ diễn ra vào 19h45 ngày Chủ nhật, 3/12/2023. Chỉ còn 3 giờ nữa thì giải đấu sẽ diễn ra, hãy thu xếp thời gian và tham gia để được trở thành chủ nhân quỹ giải thưởng vô cùng giá trị nhé!
Mọi người chỉ cần gia nhập giải đấu và đội là đã tự động đăng kí thành công rồi nhé! Đây là giải đấu diễn ra hoàn toàn online và không có lệ phí.
*Chi tiết điều lệ giải: http://bit.ly/vemcseason9
*Tham gia giải đấu tại: https://lichess.org/tournament/xOPKDKIL
*Tổng giá trị giải thưởng: hơn 20 triệu đồng, hơn 100 giải thưởng.
- 1 GIẢI NHẤT: 1.000.000đ + 100GP.
- 1 GIẢI NHÌ: 400.000đ + 50GP.
- 1 GIẢI BA: 200.000đ + 30GP.
- 2 GIẢI TƯ: 100.000đ + 20GP.
- 5 GIẢI NĂM: 50.000đ + 10GP.
- 10 GIẢI SÁU: 20.000đ + 5GP.
- 20 GIẢI KHUYẾN KHÍCH: 10.000đ + 3GP.
- NHẤT < 2000 ELO: 100.000đ.
- NHÌ < 2000 ELO: 50.000đ
- 5 GIẢI BA < 2000 ELO: 10.000đ
- NHẤT < 1500 ELO: 50.000đ.
- NHÌ < 1500 ELO: 20.000đ
- 3 GIẢI BA < 1500 ELO: 10.000đ
- NHẤT < 1200 ELO: 30.000đ
- 3 GIẢI NHÌ < 1200 ELO: 10.000đ
sự kiện hay quá
mà lại đúng môn tủ nè