Trong đề thi THPTQG 2023 môn Toán có 50 câu trắc nghiệm, mỗi câu được 0,2 điểm. Mỗi câu hỏi có 4 đáp án trắc nghiệm A,B,C,D và chỉ có 1 đáp án đúng. Điểm bé hơn hoặc bằng 1 được coi là điểm liệt. Bạn An chọn ngẫu nhiên 4 đáp án với cả 50 câu hỏi. Tính xác suất để bạn An không bị điểm liệt.
Đường link tham khảo: Có nên "khoanh lụi" thi THPTQG hay không?
https://www.youtube.com/watch?v=gETeWVaK-E8
Đúng 2
Bình luận (0)
\(n\left(\Omega\right)=4^{50}\)
Nếu bạn An bị điểm liệt thì số câu đúng mà bạn chọn được bé hơn hoặc bằng 5, hay số câu sai lớn hơn hoặc bằng 45.
Gọi biến cố A: "bạn An không bị điểm liệt"
\(n\left(\overline{A}\right)=C_{50}^{45}.3^{45}+C_{50}^{46}.3^{46}+C_{50}^{47}.3^{47}+C_{50}^{48}.3^{48}+C_{50}^{49}.3^{49}+C_{50}^{50}.3^{50}\)
Xác suất để bạn An không bị điểm liệt
\(P\left(A\right)=1-\dfrac{n\left(\overline{A}\right)}{n\left(\Omega\right)}\)
\(=1-\dfrac{C_{50}^{45}.3^{45}+C_{50}^{46}.3^{46}+C_{50}^{47}.3^{47}+C_{50}^{48}.3^{48}+C_{50}^{49}.3^{49}+C_{50}^{50}.3^{50}}{4^{50}}\)
\(\approx0,99295\)
Đúng 4
Bình luận (0)

Hãy tự tạo động lực cho mình để có một tuần học tập thật hiệu quả các em nhé!
Thật sự có nhiều lúc em mệt mỏi lắm, muốn buôn bỏ mọi thứ. Kiểu mọi thứ ập đến đội ngột lắm, đầu năm em đi ôn toán nhưng do một số chuyện giữa mẹ em và thầy toán nên ba em đã không cho em đi ôn nữa lúc đó em khóc rất nhiều luôn ấy. Nhưng mà em đã xin ba cho em tự ôn ở nhà em vẫn muốn thi tiếp rất may là ba đồng ý, sau vụ đó ngày nào em cũng thức rất khuya để giải đề. Cũng có nhiều khó khăn lắm í nhưng mà cũng có một phần nhờ các chị bên hoc24 em có nhắn tin hỏi bên nhóm hoc24 các anh chị rất nhiệt tình luôn ấy cảm động thật sự, cũng có nhiều thầy cô an ủi em lắm nên em ngày một cố gắn cùng với đó nữa em là Fan của Mono và rất hân hạnh khi được anh ấy chúc em thành công:33 và hơn nữa bạn bè em luôn động viên em nữa nè

Đúng 14
Bình luận (3)
Động lực để em cố gắng chăm chỉ mỗi ngày là những dòng tin nhắn của mẹ. Đến với môi trường mới thật khó để nhanh chóng thích nghi với những cái mới nên rất dễ gặp phải tình trạng bị mất động lực cố gắng học tập. Nhờ có mẹ luôn động viên học làm hậu phương vững chắc đã tiếp thêm cho em rất nhiều động lực chinh phục con đường học vấn mình đã chọn
Đúng 10
Bình luận (0)
em kiểu cứ nhất lớp cứ là lớp trưởng thì cái gì cũng một tay em .Đại diện lớp cũng em,trông lớp cũng em ,quản lớp cũng em ,chỉ đạo cũng em ,đi thi cũng em .Khổ cái lớp em thành tích ,ý thức ,lao động lại xếp cuối trường nên nhưng bạn cán sự lớp nhọc lắm.Mới vào năm học là lễ hội ,rồi thi,rồi khai mạc ,mới đó mà cả đống lễ hội đi thi ,em tập đến nỗi không biết là mình đã thi giữa kì 1,rồi sắp tới lại kể chuyện anh bộ đội cụ hồ chào mừng ngày 22-12 .áp lực thật sự ,điểm thi giữa kì là 1 cú sốc với em ,em chưa bao giờ có điểm thấp như vậy.nhiều lúc muốn buông xuôi ,bỏ hết tất cả ,kệ nó đi nhưng áp lực gia đình bắt em phải tiếp tục .nhiều lúc em không có thời gian rảnh để làm những việc riêng của mình luôn á.em có đi học thêm ,nhiều lúc em nghĩ sao họ học 5 ngày trên 1 tuần còn mình phải học cả tuần .KHÔNG BAO GIỜ LẠC QUAN NỔI ![]()
Đúng 5
Bình luận (2)
Xem thêm câu trả lời
THÔNG BÁO KẾT QUẢ VÒNG 1 CUỘC THI CỜ VUA VCET SUMMER22 - SEASON 3Link giải vòng 2: https://lichess.org/swiss/JmbnS98HNhững ai tham dự vòng 1: 10 điểm giải 1GP.Cú pháp nhận giải: trả lời dưới bài đăng này:Họ và tên: ................................Tên tài khoản Lichess: ............Số điểm đạt được: ..................Thứ hạng: ...............................Sau đó các bạn hãy bình luận vào câu trả lời của mình, số comment bằng số GP các bạn nhận được. Ví dụ nếu bạn được 23 điểm (nhận 2GP), hãy c...
Đọc tiếp
THÔNG BÁO KẾT QUẢ VÒNG 1 CUỘC THI CỜ VUA VCET SUMMER'22 - SEASON 3
Link giải vòng 2: https://lichess.org/swiss/JmbnS98H
Những ai tham dự vòng 1: 10 điểm giải = 1GP.
Cú pháp nhận giải: trả lời dưới bài đăng này:
Họ và tên: ................................
Tên tài khoản Lichess: ............
Số điểm đạt được: ..................
Thứ hạng: ...............................
Sau đó các bạn hãy bình luận vào câu trả lời của mình, số comment bằng số GP các bạn nhận được. Ví dụ nếu bạn được 23 điểm (nhận 2GP), hãy comment 2 lần vào câu trả lời mình.
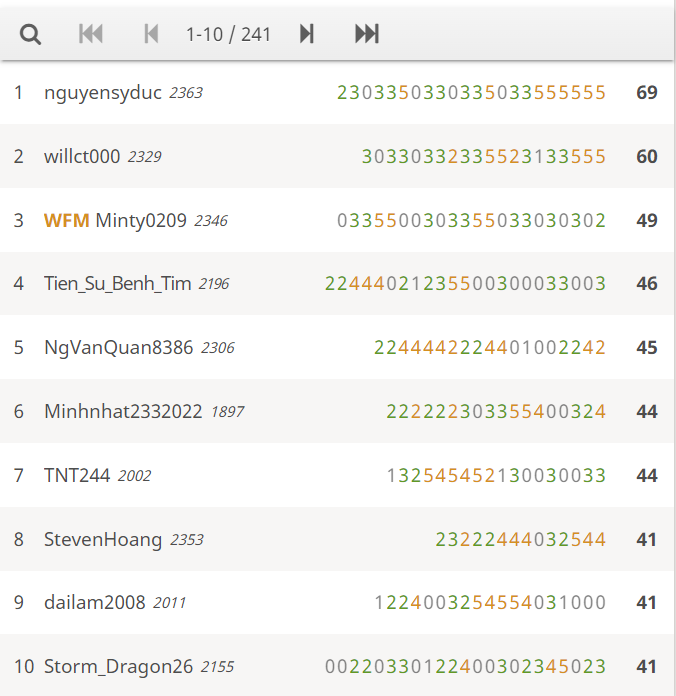
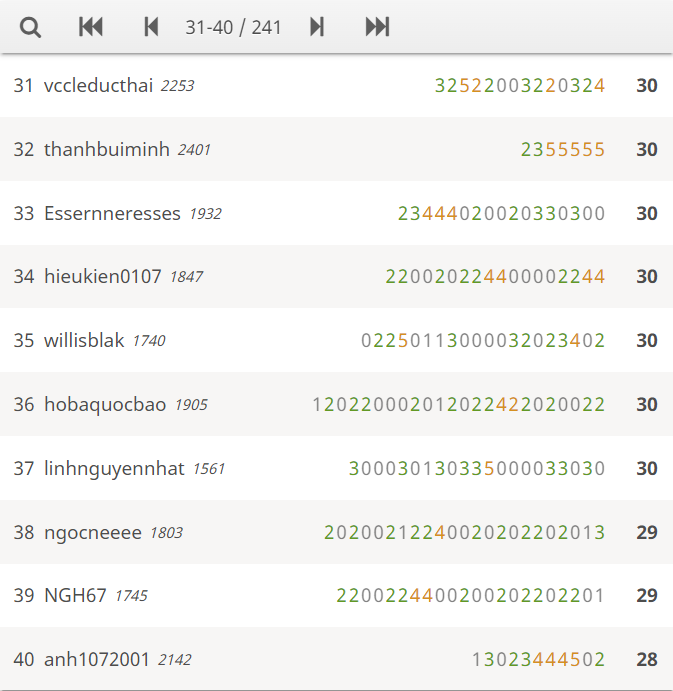
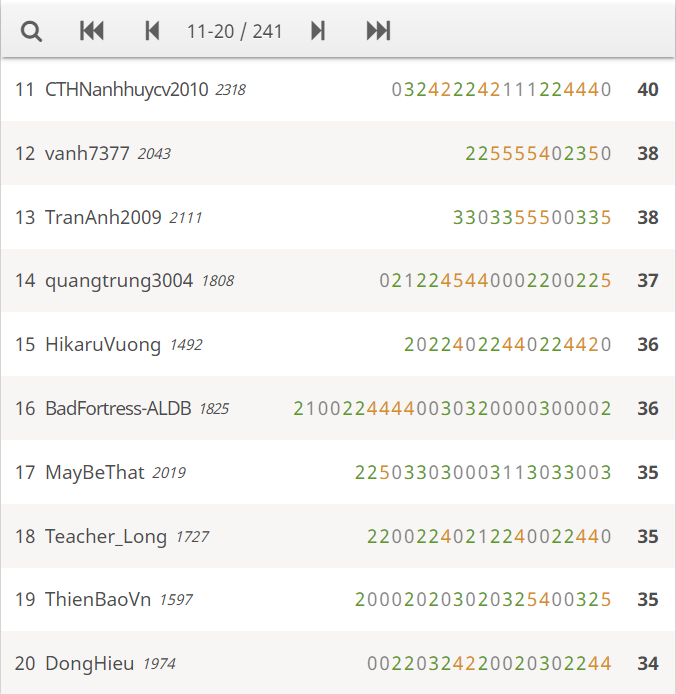
Vòng 1 Cuộc thi Cờ vua VCET Summer'22 - Season 3 đã kết thúc thành công ngoài mong đợi với 241 kì thủ tranh tài. Sau 150 phút gay cấn và kịch tính nhưng không thiếu sự vui vẻ và hòa đồng, BTC xin được công bố kết quả 80 bạn xuất sắc nhất bước tiếp vào vòng 2.
Các bạn hãy mở trang Lichess và kiểm tra ngay hộp thư của mình để nhận link tham dự vòng 2 và mật khẩu nhé. Do có một số thay đổi trong điều khoản, vòng 2 sẽ là vòng chung kết và trực tiếp xét giải thưởng chung cuộc, và chúng mình sẽ có một số thay đổi nhỏ cơ cấu giải thưởng.
Một lần nữa xin chúc mừng 80 kì thủ xuất sắc nhất! Rất mong được gặp lại các bạn trong vòng chung kết sẽ diễn ra vào 19h45 ngày 22/5/2022 (chủ nhật, 6 ngày)! Những bạn chưa vượt qua vòng 2, chúng mình còn một số hậu sự kiện có giải thưởng để các bạn tiếp tục cuộc vui với bộ môn Cờ vua đó, hãy theo dõi những tin tức mới nhất từ VICE nha!
Họ và tên: Lê Michael
Tên tài khoản Lichess: Sachinhi
Số điểm đạt được: 21
Thứ hạng: 75
Đúng 5
Bình luận (4)
Họ và tên: Phan Sơn
Tên tài khoản Lichess: TNT244
Số điểm đạt được: `44`
Thứ hạng: `7`. :D
Đúng 3
Bình luận (0)
Họ và tên: Phan Sơn
Tên tài khoản Lichess: TNT244
Số điểm đạt được: `44`
Thứ hạng: `7`. :D
Đúng 2
Bình luận (0)
Xem thêm câu trả lời
Lập công thức tổng quát tính tổng: \(C_n^0+C_n^1+...+C^k_n\). (với \(k,n\in\mathbb{N*};k\leq n\))
CHUỖI SERIES CÂU HỎI ĐỀ LUYỆN THI ĐGNL ĐHQG TPHCM
[MÔN TOÁN NGÀY 3]


Xem thêm câu trả lời
CHUỖI SERIES CÂU HỎI ĐỀ LUYỆN THI ĐGNL ĐHQG TPHCM
[TOÁN NGÀY 2]

tí tiếng anh bắt giải thích nữa chắc xỉu
Đúng 1
Bình luận (1)
Mọi người cứ làm, câu nào giải thích được thì giải thích, mình không đánh nhiều vào giải thích chỉ xem cái tư duy bài toán của mọi người ổn không, nếu không ổn thì còn sửa nè!
Đúng 1
Bình luận (0)
Xem thêm câu trả lời
Cho tui hỏi với là k với k' ???? tìm cho vui or trong trắc nghiệm khoanh sao, thầy tui tìm đkxđ khién tui bối rối
Cho k là một số tự nhiên. Chứng minh rằng:
\(C_5^0.C_{2011}^k+C_5^1.C_{2011}^{k-1}+...+C_5^5.C_{2011}^{k-5}=C_{2016}^k\)
Lời giải:
Theo nhị thức Newton:
$C^k_{2016}$ chính là hệ số của $x^k$ trong khai triển $(x+1)^{2016}(*)$
Lại có:
$(x+1)^{2016}=(x+1)^5.(x+1)^{2011}$
\(=(\sum \limits_{i=0}^5C^i_5x^i)(\sum \limits_{j=0}^{2011}C^i_{2011}x^j)\)
Hệ số $x^k$ trong khai triển này tương ứng với $0\leq i\leq 5; 0\leq j\leq 2011$ thỏa mãn $i+j=k$
Hay hệ số của $x^k$ trong khai triển $(x+1)^{2016}$ là:
$C^0_5.C^k_{2011}+C^1_5.C^{k-1}_{2011}+C^2_5C^{k-2}_{2011}+C^3_5.C^{k-3}_{2011}+C^4_5.C^{k-4}_{2011}+C^5_5.C^{k-5}_{2011}(**)$
Từ $(*); (**)$ ta có đpcm.
Đúng 2
Bình luận (0)
Cho dãy số left(a_nright) xác định bởi công thức:hept{begin{cases}a_11;a_22;na_{n+2}left(3n+2right)a_{n+1}-2left(n+1right)a_n;n1;2;3...end{cases}}a) Tìm công thức số hạng tổng quát của dãy left(a_nright)b)Chứng minh sqrt{a_1-1}+sqrt{a_2-1}+...+sqrt{a_n-1}gefrac{nleft(n+1right)}{2};forall ninℕ^∗c) Tính limleft(frac{a_1}{3}+frac{a_2}{3^2}+...+frac{a_n}{3^n}right)
Đọc tiếp
Cho dãy số \(\left(a_n\right)\) xác định bởi công thức:
\(\hept{\begin{cases}a_1=1;a_2=2;\\na_{n+2}=\left(3n+2\right)a_{n+1}-2\left(n+1\right)a_n;n=1;2;3...\end{cases}}\)
a) Tìm công thức số hạng tổng quát của dãy \(\left(a_n\right)\)
b)Chứng minh \(\sqrt{a_1-1}+\sqrt{a_2-1}+...+\sqrt{a_n-1}\ge\frac{n\left(n+1\right)}{2};\forall n\inℕ^∗\)
c) Tính \(lim\left(\frac{a_1}{3}+\frac{a_2}{3^2}+...+\frac{a_n}{3^n}\right)\)
a.
\(\Leftrightarrow na_{n+2}-na_{n+1}=2\left(n+1\right)a_{n+1}-2\left(n+1\right)a_n\)
\(\Leftrightarrow\dfrac{a_{n+2}-a_{n+1}}{n+1}=2.\dfrac{a_{n+1}-a_n}{n}\)
Đặt \(b_n=\dfrac{a_{n+1}-a_n}{n}\Rightarrow\left\{{}\begin{matrix}b_1=\dfrac{a_2-a_1}{1}=1\\b_{n+1}=2b_n\end{matrix}\right.\) \(\Rightarrow b_n=2^{n-1}\Rightarrow a_{n+1}-a_n=n.2^{n-1}\)
\(\Leftrightarrow a_{n+1}-\left[\dfrac{1}{2}\left(n+1\right)-1\right]2^{n+1}=a_n-\left[\dfrac{1}{2}n-1\right]2^n\)
Đặt \(c_n=a_n-\left[\dfrac{1}{2}n-1\right]2^n\Rightarrow\left\{{}\begin{matrix}c_1=a_1-\left[\dfrac{1}{2}-1\right]2^1=2\\c_{n+1}=c_n=...=c_1=2\end{matrix}\right.\)
\(\Rightarrow a_n=\left[\dfrac{1}{2}n-1\right]2^n+2=\left(n-2\right)2^{n-1}+2\)
Đúng 2
Bình luận (0)
b.
Câu b này đề sai
Với \(n=1\Rightarrow\sqrt{a_1-1}=0< \dfrac{1\left(1+1\right)}{2}\)
Với \(n=2\Rightarrow\sqrt{a_1-1}+\sqrt{a_2-1}=0+1< \dfrac{2\left(2+1\right)}{2}\)
Có lẽ đề đúng phải là: \(\sqrt{a_1-1}+\sqrt{a_2-1}+...+\sqrt{a_n-1}\ge\dfrac{n\left(n-1\right)}{2}\)
Ta sẽ chứng minh: \(\sqrt{a_n-1}\ge n-1\) ; \(\forall n\in Z^+\)
Hay: \(\sqrt{\left(n-2\right)2^{n-1}+1}\ge n-1\)
\(\Leftrightarrow\left(n-2\right)2^{n-1}+2n\ge n^2\)
- Với \(n=1\Rightarrow-1+2\ge1^2\) (đúng)
- Với \(n=2\Rightarrow0+4\ge2^2\) (đúng)
- Giả sử BĐT đúng với \(n=k\ge2\) hay \(\left(k-2\right)2^{k-1}+2k\ge k^2\)
Ta cần chứng minh: \(\left(k-1\right)2^k+2\left(k+1\right)\ge\left(k+1\right)^2\)
\(\Leftrightarrow\left(k-1\right)2^k+1\ge k^2\)
Thật vậy: \(\left(k-1\right)2^k+1=2\left(k-2\right)2^{k-1}+2^k+1\ge2k^2-4k+2^k+1\)
\(\ge2k^2-4k+5=k^2+\left(k-2\right)^2+1>k^2\) (đpcm)
Do đó:
\(\sqrt{a_1-1}+\sqrt{a_2-1}+...+\sqrt{a_n-1}>0+1+...+n-1=\dfrac{n\left(n-1\right)}{2}\)
Đúng 2
Bình luận (0)
c.
Ta có:
\(\dfrac{a_n}{3^n}=\dfrac{\left(n-2\right)2^{n-1}+2}{3^n}=\dfrac{n}{2\left(\dfrac{3}{2}\right)^n}-\left(\dfrac{2}{3}\right)^n+\dfrac{2}{3^n}\)
Đặt \(S_n=\sum\limits^n_{i=1}\dfrac{a_n}{3^n}=\dfrac{1}{2}\sum\limits^n_{i=1}\dfrac{n}{\left(\dfrac{3}{2}\right)^n}-\sum\limits^n_{j=1}\left(\dfrac{2}{3}\right)^n+2\sum\limits^n_{k=1}\dfrac{1}{3^n}=\dfrac{1}{2}S'-2+2\left(\dfrac{2}{3}\right)^n+1-\dfrac{1}{3^n}\)
Xét \(S'=\sum\limits^n_{i=1}\dfrac{n}{\left(\dfrac{3}{2}\right)^n}\)
\(S'=\sum\limits^n_{i=1}\dfrac{n}{\left(\dfrac{3}{2}\right)^n}=\dfrac{1}{\dfrac{3}{2}}+\dfrac{2}{\left(\dfrac{3}{2}\right)^2}+\dfrac{3}{\left(\dfrac{3}{2}\right)^3}+...+\dfrac{n}{\left(\dfrac{3}{2}\right)^n}\)
\(\dfrac{3}{2}S'=1+\dfrac{2}{\dfrac{3}{2}}+\dfrac{3}{\left(\dfrac{3}{2}\right)^2}+...+\dfrac{n}{\left(\dfrac{3}{2}\right)^{n-1}}\)
\(\Rightarrow\dfrac{1}{2}S'=1+\dfrac{1}{\left(\dfrac{3}{2}\right)}+\dfrac{1}{\left(\dfrac{3}{2}\right)^2}+...+\dfrac{1}{\left(\dfrac{3}{2}\right)^{n-1}}-\dfrac{n}{\left(\dfrac{3}{2}\right)^n}=\dfrac{1-\left(\dfrac{2}{3}\right)^n}{1-\dfrac{2}{3}}=3-3\left(\dfrac{2}{3}\right)^n-n\left(\dfrac{2}{3}\right)^n\)
\(\Rightarrow S_n=2-\left(\dfrac{2}{3}\right)^n-\dfrac{1}{3^n}-n\left(\dfrac{2}{3}\right)^n\)
\(\Rightarrow\lim\left(S_n\right)=2\)
Đúng 3
Bình luận (0)
Tìm tất cả hàm số f:Z+->Z+ thoả mãn \(f(f(n)/n\)2020)=n2021, với mọi số nguyên dương n





























