a: \(Q=\left(x^2+2\right)^2-\left(x-2\right)\left(x+2\right)\left(x^2+4\right)\)

\(=\left(x^2+2\right)^2-\left(x^2-4\right)\left(x^2+4\right)\)

\(=x^4+4x^2+4-x^4+16=4x^2+20\)

|x|=2

=>\(x^2=\left(\left|x\right|\right)^2=2^2=4\)

Thay \(x^2=4\) vào Q, ta được:

\(Q=4\cdot4+20=16+20=36\)

b: \(4x^2>=0\forall x\)

=>\(4x^2+20>=20>0\forall x\)

=>\(Q>0\forall x\)

=>Q luôn dương với mọi x

a) Biểu thức thời gian hoàn thành công việc theo kế hoạch: \(t\left(kế.hoạch\right)=\dfrac{600}{x}\left(giờ\right)\)

b) Biểu thức thời gian hoàn thành công việc thực tế:

\(t\left(thực.tế\right)=\dfrac{600}{x+20}\left(giờ\right)\)

c) Biểu thức thời gian tổ sản xuất hoàn thành công việc trước kế hoạch:

\(\Delta t=t\left(kế.hoạch\right)-t\left(thực.tế\right)\)

\(\Rightarrow\Delta t==\dfrac{600}{x}-\dfrac{600}{x+2}=\dfrac{12000}{x\left(x+2\right)}\left(giờ\right)\)

d) Thời gian hoàn thành công việc theo kế hoạch: \(\dfrac{600}{50}=12\left(giờ\right)\)

Thời gian hoàn thành công việc thực tế, với năng suất thực tế \(50+20=70\left(chiếc/giờ\right)\) là \(\dfrac{600}{70}=\dfrac{60}{7}\approx8,57\left(giờ\right)\)

Thời gian hoàn thành công việc trước kế hoạch:

\(12-\dfrac{60}{7}=\dfrac{24}{7}\approx3,43\left(giờ\right)\)

a: \(Q=\left(x^2+2\right)^2-\left(x-2\right)\left(x+2\right)\left(x^2+4\right)\)

\(=\left(x^2+2\right)^2-\left(x^2-4\right)\left(x^2+4\right)\)

\(=x^4+4x^2+4-x^4+16=4x^2+20\)

|x|=2

=>\(x^2=\left(\left|x\right|\right)^2=2^2=4\)

Thay \(x^2=4\) vào Q, ta được:

\(Q=4\cdot4+20=16+20=36\)

b: \(4x^2>=0\forall x\)

=>\(4x^2+20>=20>0\forall x\)

=>\(Q>0\forall x\)

=>Q luôn dương với mọi x

a: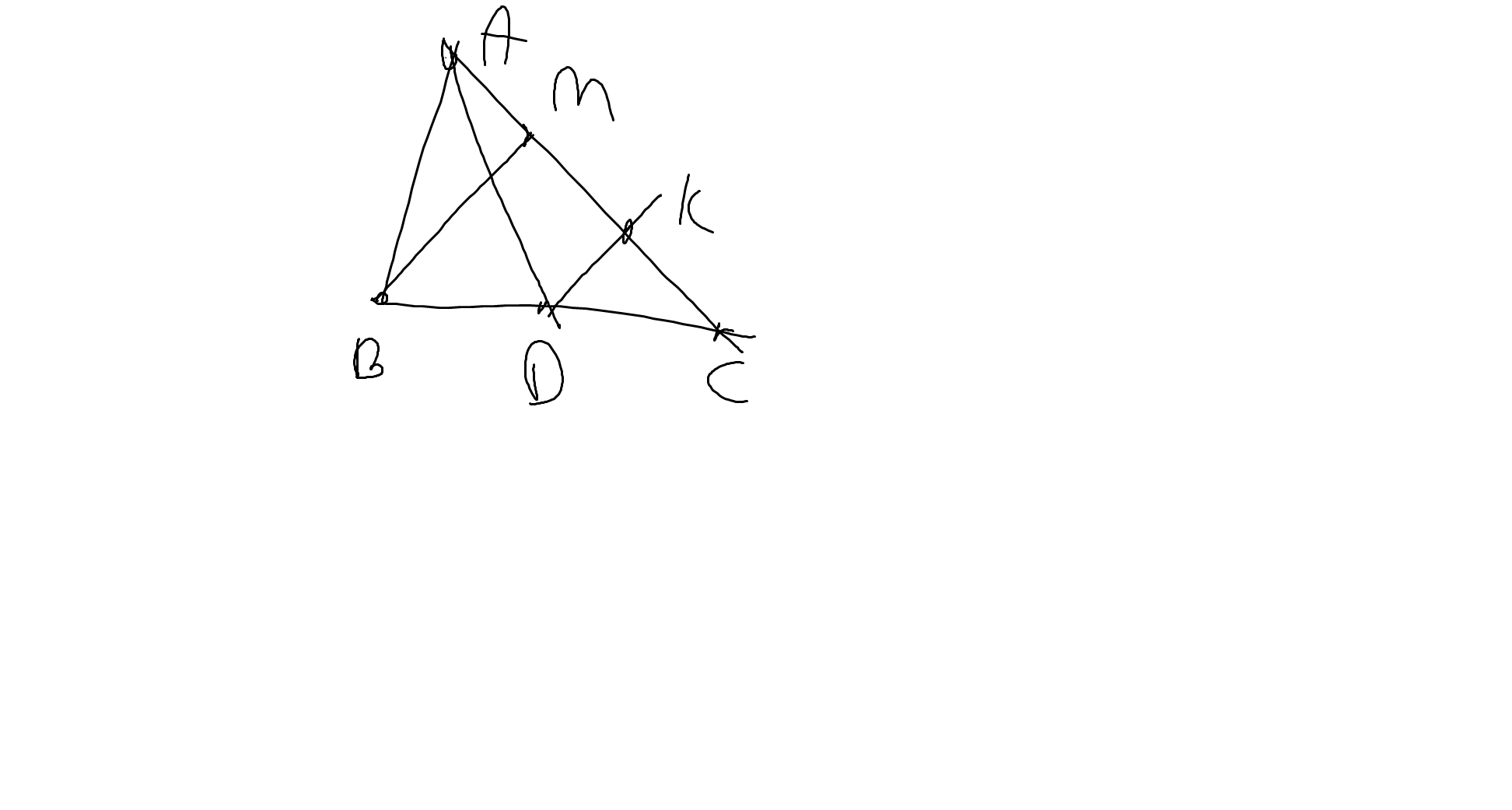 

b: Gọi K là trung điểm của MC

=>\(MK=KC=\dfrac{MC}{2}\)

mà \(AM=\dfrac{1}{2}MC\)

nên AM=MK=KC

Vì AM=MK nên M là trung điểm của AK

Xét ΔBMC có

D,K lần lượt là trung điểm của CB,CM

=>DK là đường trung bình của ΔBMC

=>DK//BM và DK=1/2BM

=>OM//DK

Xét ΔADK có

M là trung điểm của AK

MO//DK

Do đó: O là trung điểm của AD

c: Xét ΔADK có 

O,M lần lượt là trung điểm của AD,AK

=>OM là đường trung bình của ΔADK

=>\(OM=\dfrac{1}{2}DK\)

=>\(OM=\dfrac{1}{2}\cdot\dfrac{1}{2}\cdot BM=\dfrac{1}{4}BM\)

a: Xét tứ giác AMHN có \(\widehat{AMH}=\widehat{ANH}=\widehat{MAN}=90^0\)

nên AMHN là hình chữ nhật

=>AH=MN

b: AMHN là hình chữ nhật

=>AH cắt MN tại trung điểm của mỗi đường

=>O là trung điểm chung của AH và MN

Ta có: AMHN là hình chữ nhật

=>AN//HM và AN=HM

AN//HM nên HM//PN

AN=HM

mà AN=NP

nên HM=NP

Xét tứ giác HMNP có

HM//NP

HM=NP

Do đó: HMNP là hình bình hành

=>MN//HP

Xét ΔHAC có

O,J lần lượt là trung điểm của HA,HC

=>OJ là đường trung bình của ΔHAC

=>OJ//AC

HMNP là hình bình hành

=>HN cắt MP tại trung điểm của mỗi đường

=>I là trung điểm chung của HN và MP

Xét ΔMNP có

O,I lần lượt là trung điểm của MN,MP

=>OI là đường trung bình của ΔMNP

=>OI//PN

=>OI//AC

mà OJ//AC

và OI,JO có điểm chung là O

nên O,I,J thẳng hàng

\(A=x^2-2xy+2y^2+2x-10y+33\)

\(\Rightarrow A=\left(x^2+y^2+1-2xy+2x-2y\right)+\left(y^2-8y+16\right)+17\)

\(\Rightarrow A=\left(x-y+1\right)^2+\left(y-4\right)^2+17\ge17\)

Dấu "=" xảy ra khi và chỉ khi 

\(\left\{{}\begin{matrix}x-y+1=0\\y-4=0\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}x=3\\y=4\end{matrix}\right.\)

Vậy \(GTNN\left(A\right)=17\left(tại.\left(x;y\right)=\left(3;4\right)\right)\)

Bài 1:

a: ĐKXĐ: \(x^2-1\ne0\)

=>\(x^2\ne1\)

=>\(x\notin\left\{1;-1\right\}\)

b:

\(B=\dfrac{2x+2}{x^2-1}=\dfrac{2\left(x+1\right)}{\left(x-1\right)\left(x+1\right)}=\dfrac{2}{x-1}\)

Thay x=2 vào B, ta được:

\(B=\dfrac{2}{2-1}=\dfrac{2}{1}=2\)

Vì x=1 không thỏa mãn ĐKXĐ nên khi x=1 thì B không có giá trị

Bài 2:

a: ĐKXĐ: \(x\ne2\)

b: Thay x=1;y=2 vào B, ta được:

\(B=\dfrac{8\cdot1+3\cdot2}{4\cdot1-8}=\dfrac{8+6}{4-8}=\dfrac{14}{-4}=-\dfrac{7}{2}\)

Thay x=3;y=4 vào B, ta được:

\(B=\dfrac{8\cdot3+3\cdot4}{4\cdot3-8}=\dfrac{24+12}{12-8}=\dfrac{36}{4}=9\)

a: Ta có; ΔABC vuông tại A

mà AO là đường trung tuyến

nên OA=OB=OC

OA=OB nên ΔOAB cân tại O

Xét ΔOAM vuông tại A và ΔOBM vuông tại B có

OM chung

OA=OB

do đó: ΔOAM=ΔOBM

=>MA=MB

=>M nằm trên đường trung trực của AB(1)

Ta có: OA=OB

=>O nằm trên đường trung trực của AB(2)

Từ (1),(2) suy ra MO là đường trung trực của AB

=>MO\(\perp\)AB tại E và E là trung điểm của AB

Xét ΔABC có

O là trung điểm của BC

OF//AB

Do đó: F là trung điểm của AC

Ta có: OF//AB

AB\(\perp\)AC

Do đó: OF\(\perp\)AC tại F

Xét tứ giác AEOF có \(\widehat{AEO}=\widehat{AFO}=\widehat{FAE}=90^0\)

nên AEOF là hình chữ nhật

=>AO=EF

1: ΔABC vuông tại A

mà AM là đường trung tuyến

nên MA=MB=MC

=>MA=MB

Xét tứ giác AMBN có

H là trung điểm chung của AB và MN

=>AMBN là hình bình hành

Hình bình hành AMBN có MA=MB

nên AMBN là hình thoi

2: AMBN là hình thoi

=>BM=BN và BA là phân giác của góc MBN

Xét ΔDMB và ΔDNB có

BM=BN

\(\widehat{DBM}=\widehat{DBN}\)

BD chung

Do đó: ΔDMB=ΔDNB

=>\(\widehat{DMB}=\widehat{DNB}\)

=>\(\widehat{DMB}=90^0\)

=>DM\(\perp\)BC

Xét ΔDBC có

DM là đường cao

DM là đường trung tuyến

Do đó: ΔDBC cân tại D