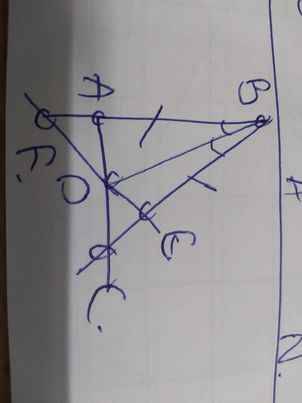
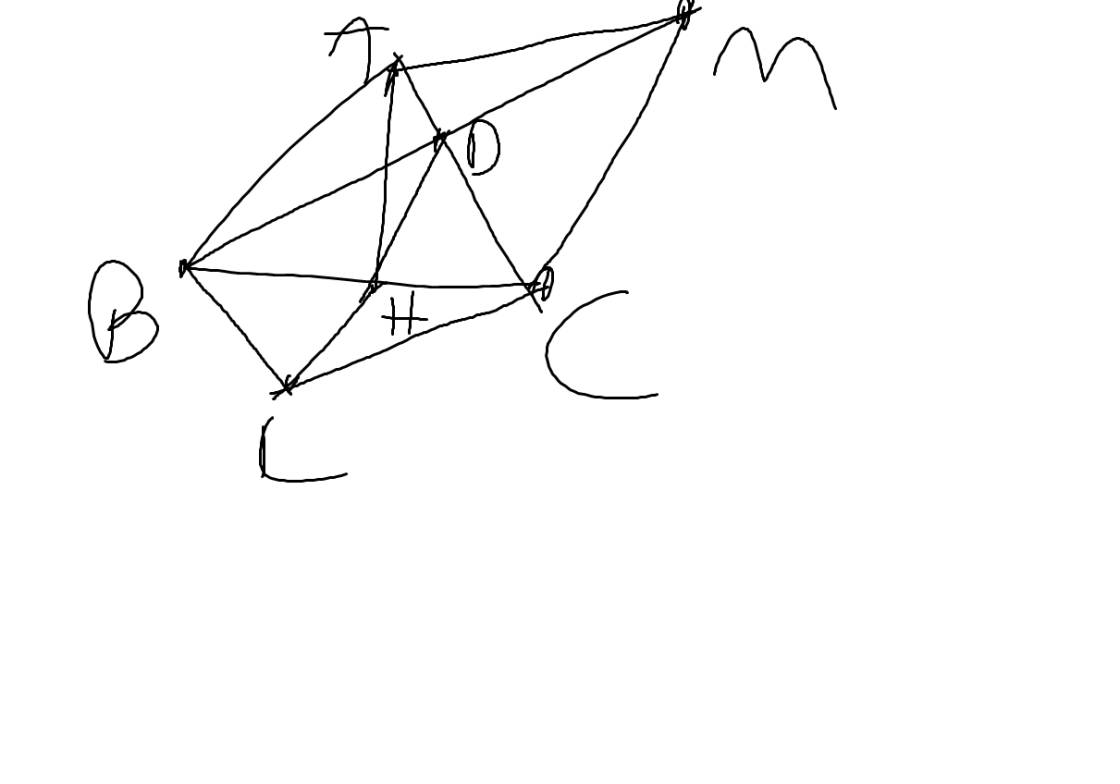
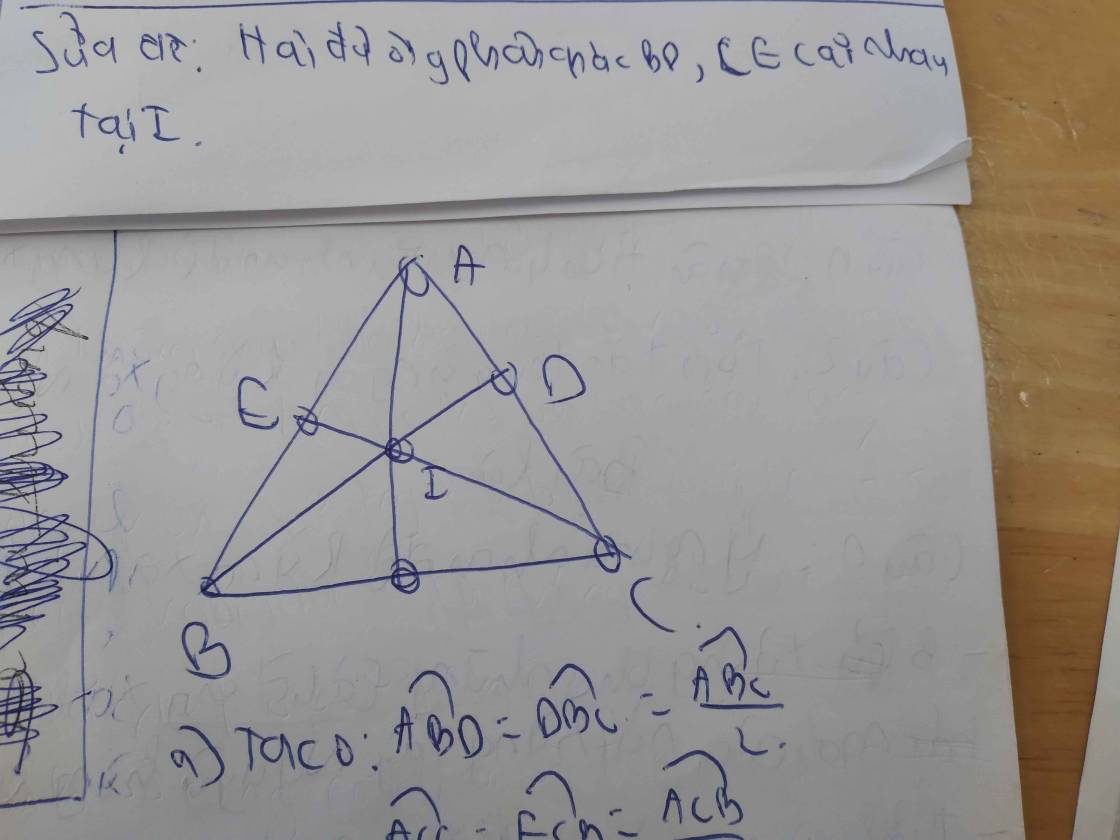
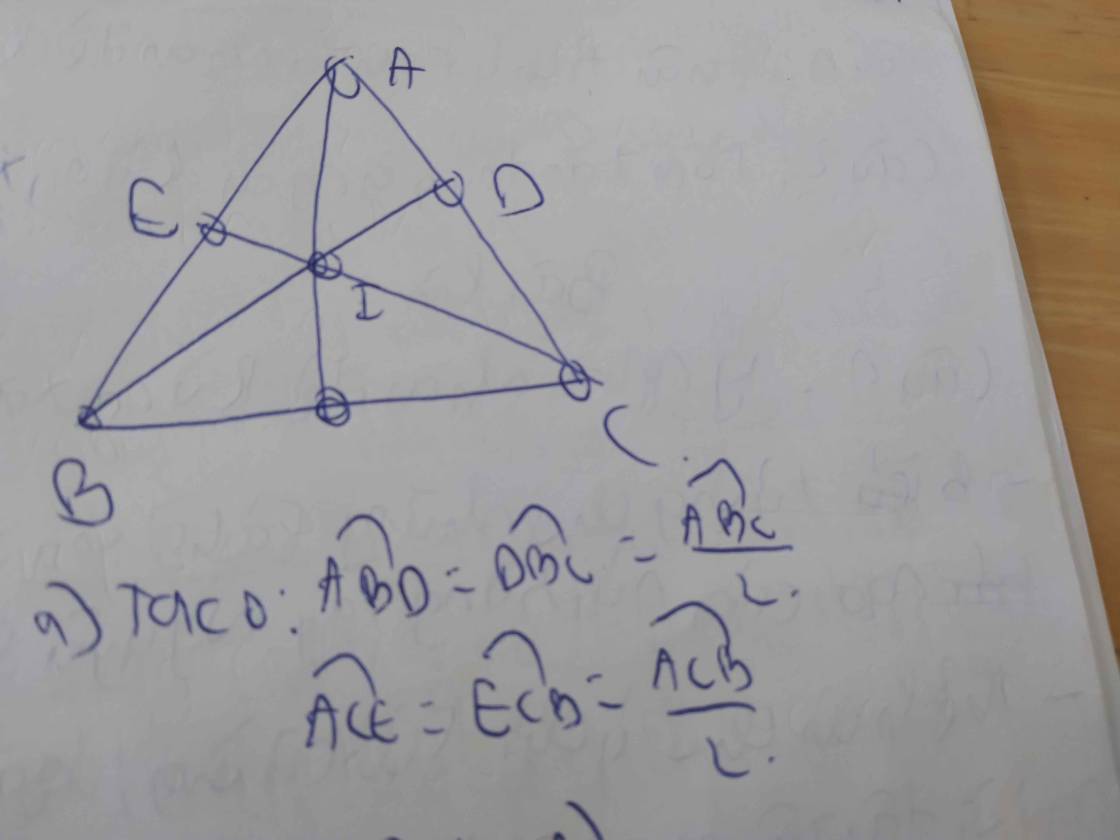
Cho tam giác ABC vuông tại A. Kẻ BD là phân giác của ABC (D ϵ AC). Trên đoạn BC lấy điểm E sao cho AB = BE
a, Chứng minh AD = DE
b, Trên tia đối của tia AB lấy điểm F sao cho AF = EC. Chứng minh BD vuông FC
c, Chứng minh AF // FC
d, Chứng minh ba điểm D, E, F thẳng hàng