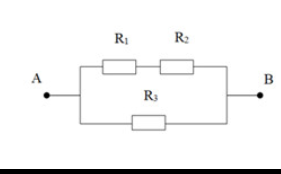
Tóm tắt sơ đồ:
\(\left[\left(R_1nt\left(R_2//R_4\right)\right)//R_3\right]\)
\(R_2+R_4=\dfrac{5.5}{5+5}=2,5\left(\Omega\right)\)
\(R_2+R_2+R_4=2,5+9,5=12\left(\Omega\right)\)
\(R_m=\dfrac{12.4}{12+4}=3\left(\Omega\right)\)
-> A
Vẽ lại mạch như sau:
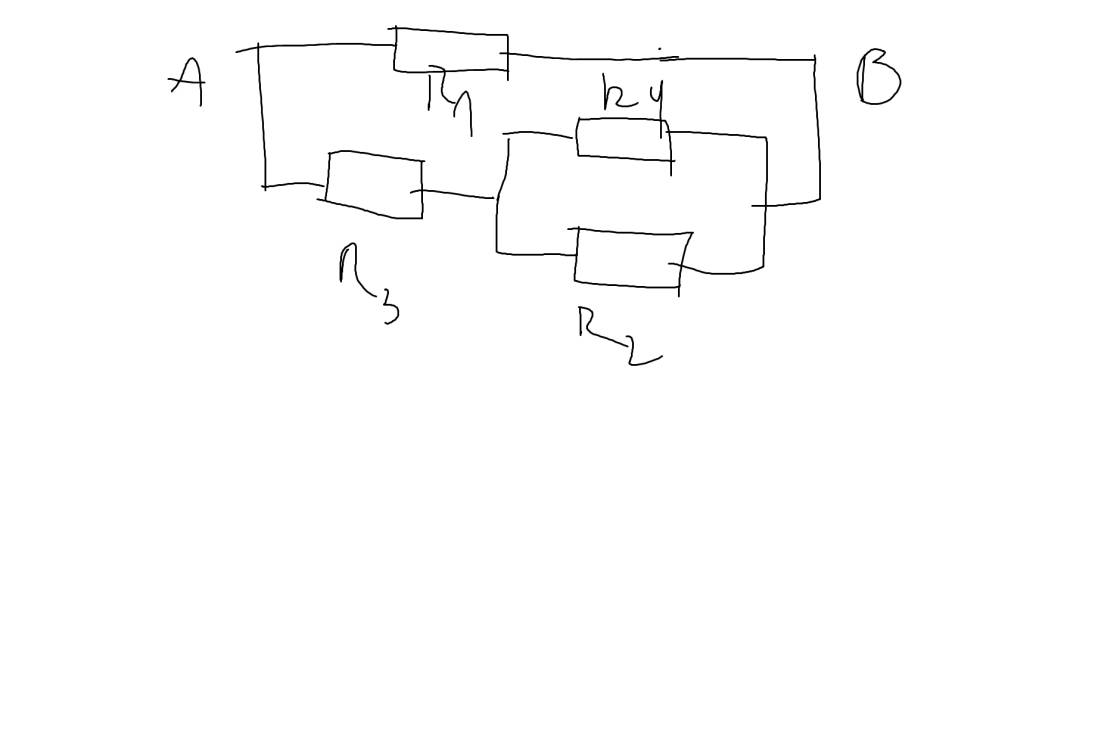
Do đó, ta có sơ đồ: R1//(R3 nt(R4//R2))
R4//R2 nên \(R_{24}=\dfrac{R_2\cdot R_4}{R_2+R_4}=\dfrac{5\cdot5}{5+5}=\dfrac{25}{10}=2,5\left(\Omega\right)\)
R3 nt R42 nên \(R_{342}=R_3+R_{24}=2,5+4=6,5\Omega\)
R1//R234 nên \(R=\dfrac{R_1\cdot R_{234}}{R_1+R_{234}}=\dfrac{9,5\cdot6,5}{9,5+6,5}=3,859375\left(\Omega\right)\simeq4\Omega\)
=>Chọn B

.jpg)