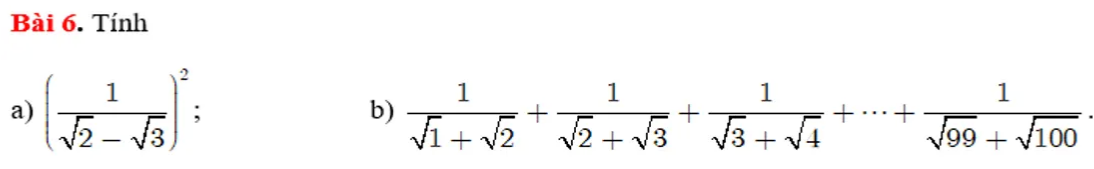\(a.\left(\dfrac{1}{\sqrt{2}-\sqrt{3}}\right)^2\)
= \(\dfrac{1^2}{\left(\sqrt{2}-\sqrt{3}\right)^2}\)
= \(\dfrac{1}{2-3}\)
= -1
Lời giải:
a.
\(A=\left(\frac{(\sqrt{3}-\sqrt{2})(\sqrt{3}+\sqrt{2})}{\sqrt{2}-\sqrt{3}}\right)^2=[-(\sqrt{3}+\sqrt{2})]^2=(\sqrt{3}+\sqrt{2})^2=5+2\sqrt{6}\)
b.
Xét số hạng tổng quát:
\(\frac{1}{\sqrt{n}+\sqrt{n+1}}=\frac{\sqrt{n+1}-\sqrt{n}}{(\sqrt{n+1}-\sqrt{n})(\sqrt{n+1}+\sqrt{n})}=\frac{\sqrt{n+1}-\sqrt{n}}{(n+1)-n}=\sqrt{n+1}-\sqrt{n}\)
Áp dụng vào bài toán:
$B=\sqrt{2}-\sqrt{1}+\sqrt{3}-\sqrt{2}+\sqrt{4}-\sqrt{3}+....+\sqrt{100}-\sqrt{99}$
$=\sqrt{100}-\sqrt{1}=10-1=9$
a) \(\left(\dfrac{1}{\sqrt{2}-\sqrt{3}}\right)^2=\dfrac{1}{\left(\sqrt{2}-\sqrt{3}\right)^2}=\dfrac{1}{5-2\sqrt{6}}=\dfrac{5+2\sqrt{6}}{\left(5-2\sqrt{6}\right)\left(5+2\sqrt{6}\right)}=\dfrac{5+2\sqrt{6}}{1}=5+2\sqrt{6}\)
\(\left(\dfrac{1}{\sqrt{2}-\sqrt{3}}\right)^2=\dfrac{1}{\left(\sqrt{2}-\sqrt{3}\right)^2}=\dfrac{1}{5-2\sqrt{6}}\)
\(\dfrac{1}{\sqrt{1}+\sqrt{2}}+\dfrac{1}{\sqrt{2}+\sqrt{3}}+\dfrac{1}{\sqrt{3}+\sqrt{4}}+...+\dfrac{1}{\sqrt{99}+\sqrt{100}}=\dfrac{\sqrt{1}-\sqrt{2}}{-1}+\dfrac{\sqrt{2}-\sqrt{3}}{-1}+\dfrac{\sqrt{3}-\sqrt{4}}{-1}+...+\dfrac{\sqrt{99}-\sqrt{100}}{-1}=-\left(\sqrt{1}-\sqrt{2}+\sqrt{2}-\sqrt{3}+\sqrt{3}-\sqrt{4}+...+\sqrt{99}-\sqrt{100}\right)=-\sqrt{1}+\sqrt{100}\)