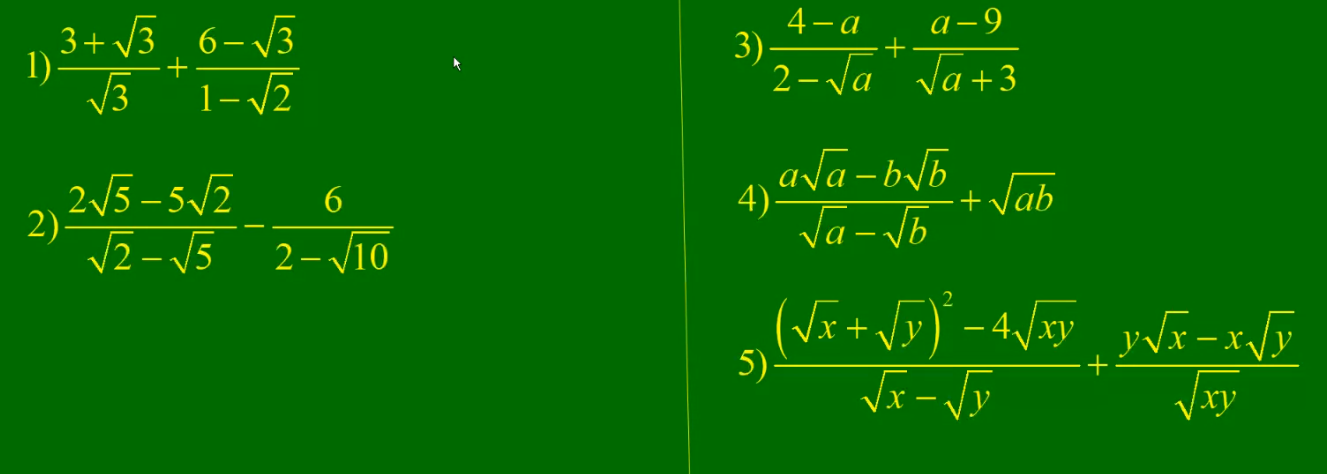1) Ta có: \(\dfrac{3+\sqrt{3}}{\sqrt{3}}+\dfrac{6-\sqrt{3}}{1-\sqrt{2}}\)
\(=\dfrac{\sqrt{3}\left(\sqrt{3}+1\right)}{\sqrt{3}}-\dfrac{\sqrt{3}\left(2\sqrt{3}-1\right)}{\sqrt{2}-1}\)
\(=\sqrt{3}+1-\left(6-\sqrt{3}\right)\left(\sqrt{2}+1\right)\)
\(=\sqrt{3}+1-6\sqrt{2}-6+\sqrt{6}+\sqrt{3}\)
\(=-5-6\sqrt{2}+\sqrt{6}+2\sqrt{3}\)
2) Ta có: \(\dfrac{2\sqrt{5}-5\sqrt{2}}{\sqrt{2}-\sqrt{5}}-\dfrac{6}{2-\sqrt{10}}\)
\(=\dfrac{\sqrt{10}\left(\sqrt{2}-\sqrt{5}\right)}{\sqrt{2}-\sqrt{5}}+\dfrac{6\left(\sqrt{10}-2\right)}{\left(\sqrt{10}-2\right)\left(\sqrt{10}+2\right)}\)
\(=\sqrt{10}+\sqrt{10}-2=2\sqrt{10}-2\)
Câu nào đây bạn ?
P/s: Chỉ đc hỏi 1 câu thôi nhé!
1. \(\dfrac{3+\sqrt{3}}{\sqrt{3}}+\dfrac{6-\sqrt{3}}{1-\sqrt{2}}\)
\(=\sqrt{3}+1-\sqrt{3}\)
= 1
2) \(\dfrac{2\sqrt{5}-5\sqrt{2}}{\sqrt{2}-\sqrt{5}}-\dfrac{6}{2-\sqrt{10}}=\dfrac{\sqrt{10}\left(\sqrt{2}-\sqrt{5}\right)}{\sqrt{2}-\sqrt{5}}-\dfrac{3\sqrt{2}}{\sqrt{2}-\sqrt{5}}\)
\(=\sqrt{10}-\dfrac{3\sqrt{2}\left(\sqrt{2}+\sqrt{5}\right)}{\left(\sqrt{2}-\sqrt{5}\right)\left(\sqrt{2}+\sqrt{5}\right)}=\sqrt{10}-\dfrac{3\sqrt{2}\left(\sqrt{2}+\sqrt{5}\right)}{-3}\)
\(=\sqrt{10}+\sqrt{2}\left(\sqrt{2}+\sqrt{5}\right)=\sqrt{10}+2+\sqrt{10}=2+2\sqrt{10}\)
3) Ta có: \(\dfrac{4-a}{2-\sqrt{a}}+\dfrac{a-9}{\sqrt{a}+3}\)
\(=2+\sqrt{a}+\sqrt{a}-3\)
\(=2\sqrt{a}-1\)
4) Ta có: \(\dfrac{a\sqrt{a}-b\sqrt{b}}{\sqrt{a}-\sqrt{b}}+\sqrt{ab}\)
\(=a+\sqrt{ab}+b+\sqrt{ab}\)
\(=a+2\sqrt{ab}+b\)
5) Ta có: \(\dfrac{\left(\sqrt{x}+\sqrt{y}\right)^2-4\sqrt{xy}}{\sqrt{x}-\sqrt{y}}+\dfrac{y\sqrt{x}-x\sqrt{y}}{\sqrt{xy}}\)
\(=\dfrac{\left(\sqrt{x}-\sqrt{y}\right)^2}{\sqrt{x}-\sqrt{y}}+\dfrac{\sqrt{xy}\left(\sqrt{y}-\sqrt{x}\right)}{\sqrt{xy}}\)
\(=\sqrt{x}-\sqrt{y}+\sqrt{y}-\sqrt{x}\)
=0