[ Tổng hợp kiến thức Toán Học dành cho HỌC SINH THCS (Part1) ]
|-----------------------------------------------------------------------------|
 #Lưu ý: Khi đọc các mục dưới đây chỉ có thể giúp các bạn cải thiện kiến thức môn Toán của mình và không bị "Mất gốc" trong môn Toán ở cấp độ THCS
#Lưu ý: Khi đọc các mục dưới đây chỉ có thể giúp các bạn cải thiện kiến thức môn Toán của mình và không bị "Mất gốc" trong môn Toán ở cấp độ THCS
(1) Phần số học:
+ Tập hợp, số phần tử, cách chỉ ra tính chất đặc trưng, tổng dãy,...
Trong toán học tập hợp gồm có các phần tử có đặt điểm chung nào đó, để kí hiệu 1 tập hợp ta dùng các chữ cái in hoa: A, B, C, D,... để gọi tên chung cho tập hợp đó như tập hợp A, B,... sau đó dùng dấu " = " và dấu { } để biểu diễn các phần tử của tập hợp trong đó để ngăn cách phẩn tử 1 với phần tử 2 ta dùng dấu " ; "
VD: Viết tập hợp A gồm các số tự nhiên nhỏ hơn 10 (1)
\(A=\left\{0;1;2;3;4;5;6;7;8;9\right\}\)
Để chỉ ra tính chất đặt trưng của 1 tập hợp ta chú ý vào yêu cầu của tập hợp:
VD: Trong để (1) có tập hợp A gồm các số " tự nhiên " nên ta khẳng định \(x\in N^+\) (x là các phần tử của A
Và là các số nhỏ hơn 10 nên: \(x< 10\) ta viết như sau:
\(A=\left\{x\in N|x< 10\right\}\)
Để tính số phần tử của 1 tập hợp ta có công thức:
(phần tử lớn nhất - phần tử nhỏ nhất) : số bước + 1
+ Số bước là khoảng cách giữa hai phần tử: 1; 2; 3; ... ⇒ số bước là: 1
Tính tổng của dãy số cách đều ta có công thức:
(phần tử lớn nhất + phần tử nhỏ nhất) x số phần tử : 2
+ Lũy thừa, nhân; chia lũy thừa, ...
Lũy thừa gồm có 2 phần: cơ số và số mũ
VD: \(2^3\) trong đó:
Cơ số: 2
Số mũ: 3
Tính lũy thừa: \(2^3=2\cdot2\cdot2=8\)
- Nhân, chia lũy thừa cùng cơ số:
Ta có: \(a^m\) và \(a^n\) có cùng cơ số a
Để nhân hai lũy thừa này ta có công thức tổng quát như sau:
\(a^m\cdot a^n=a^{m+n}\)
Tương tự khi chia hai lũy thừa này ta có công thức tổng quát:
\(a^m:a^n=a^{m-n}\)
- Nhân chia lũy thừa cùng số mũ:
Ta có hai lũy thừa: \(m^a\) và \(n^a\) có cùng số mũ a
Để nhân 2 lũy thừa này công thức tổng quát:
\(m^a\cdot n^a=\left(m\cdot n\right)^a\)
Để chia 2 lũy thừa này ta có công thức tổng quát:
\(m^a:n^a=\left(m:n\right)^a\)
Chú ý: nếu lũy thừa đó có số mũ chẵn thì lũy thừa đó luôn dương
(2) Phần hình học
+ Góc, góc nhọn, tù, vuông, bẹt,...
Góc là những gì nằm giữa hai đường thẳng cắt nhau tại 1 điểm:
VD: 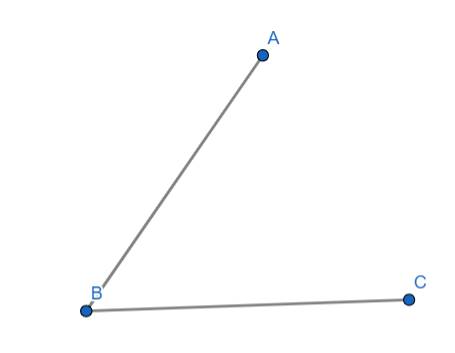
Để kí hiệu tên của một góc có hai cách:
C1: ∠ABC gọi tên góc ABC
C2: \(\widehat{ABC}\) gọi tên góc ABC
Có 4 loại góc:
- Góc nhọn: là góc có số đo nhỏ hơn 90o
- Góc tù: là góc có số đo lớn hơn 90o
- Góc vuông: là góc có số đo bằng 90o
- Góc bẹt: là góc có số đo bằng 180o
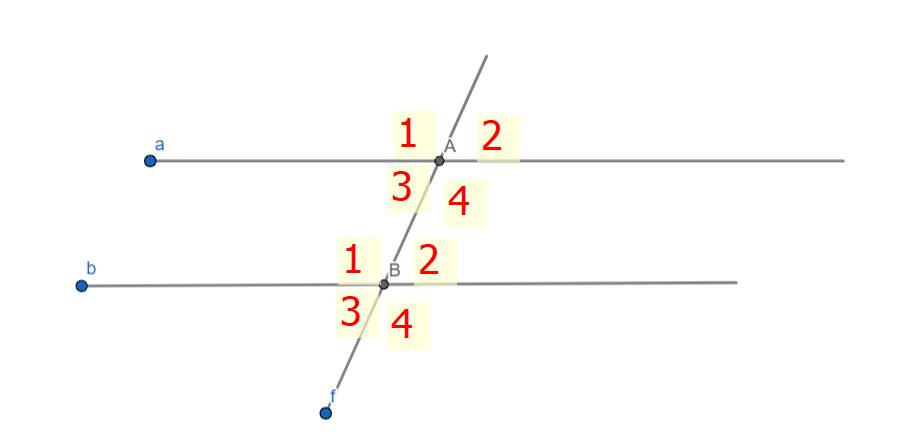
+ Hai góc kề, kề bù, phụ nhau, đối đỉnh,...
- Hai góc kề nhau là hai góc có chung 1 cạnh và có hai cạnh kia ở hai mặt phẳng khác nhau có bờ là cạnh chung
VD:
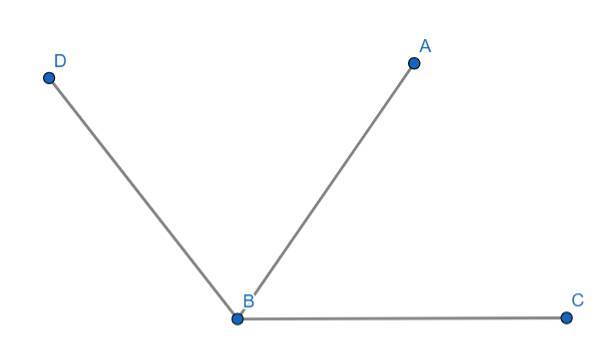
Trong đó:
\(\widehat{ABC}\) và \(\widehat{\text{D}BA}\) kề nhau và tổng số đó của hai góc này sẽ bằng số đo của góc lớn mà chũng tạo thành
\(\Rightarrow\widehat{ABC}+\widehat{DBA}=\widehat{DBC}\)
- Hai góc kề bù là hai góc có tổng số đo là 180o hay tổng của hai góc đó sẽ tạo thành 1 góc bẹt
VD:
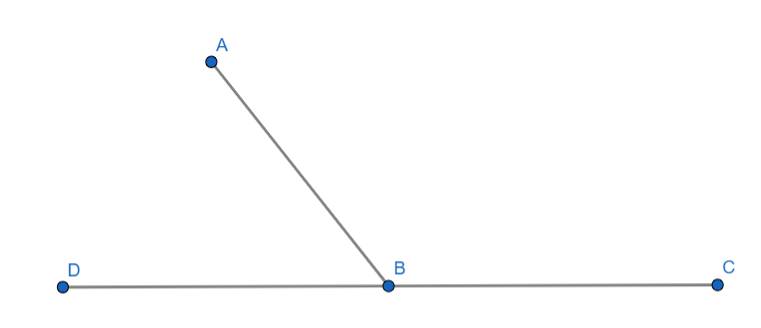
Trong đó:
\(\widehat{DBA}\) và \(\widehat{ABC}\) là hai bù nhau tổng của hai góc là 180o
\(\Rightarrow\widehat{DBA}+\widehat{ABC}=180^o=\widehat{DBC}\) (Do hai góc đồng thời cũng là hai góc kề nhau)
- Hai góc phụ nhau là hai góc có tổng số đo là: 90o hay tổng số đo của hai góc đó sẽ tạo thành 1 góc vuông
VD:
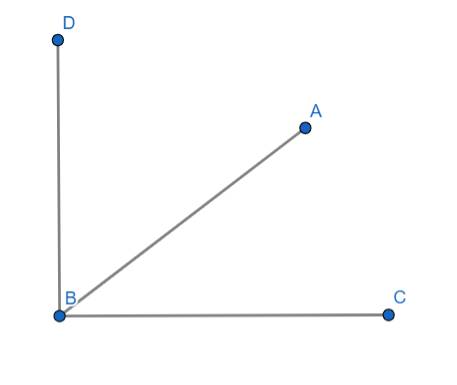
Trong đó:
\(\widehat{DBA}\) và \(\widehat{ABC}\) là hai góc phụ nhau
\(\Rightarrow\widehat{DBA}+\widehat{ABC}=90^o=\widehat{DBC}\) (Do hai góc đồng thời cũng là hai góc kề nhau)
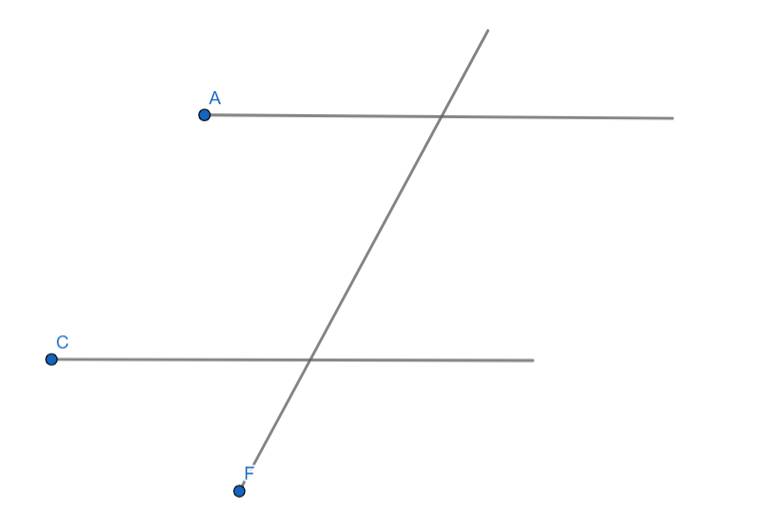
- Hai góc đổi đỉnh là hai góc có số đo góc bằng nhau mà cạnh của góc này này là tia đối của góc kia
VD:
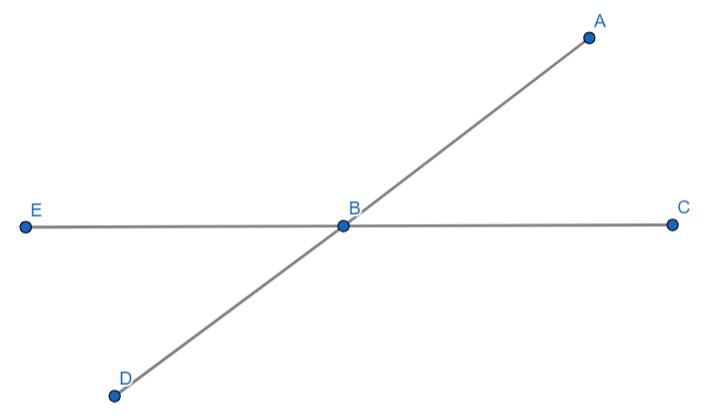
Khi đó: CE và AD cắt nhau tại B tạo ra các cặp góc đối đỉnh bằng nhau:
\(\widehat{EBD}=\widehat{ABC}\)
\(\widehat{EBA}=\widehat{DBC}\)
__________________________________________________________
(* Nếu trong part 1 này có gì thiếu sót thì mong các anh chị và các bạn góp ý với mình nhé mình sẽ cải thiện điều đó trong các part tới ạ *)
Mình có góp ý nhé
Phần tập hợp
Trong một tập hợp ta có thể dùng dấu "," hoặc ";".
Nếu trong một tập hợp mà các phần đề là chữ ta nên dùng dấu "," (bạn nào viết dấu ";" vô cũng được nhé).
Còn trong tập hợp mà các phần tử đều là số thì ta nên dùng dấu ";" ( vì nếu dùng dấu "," thì ta sẽ hơi bị rối mắt và đôi khi sẽ có nhầm lẫn).
Tuyệt quá em ơi!
Beside, bạn nào muốn mình chia sẻ ôn thi môn chuyên là Toán hay là kinh nghiệm thi chuyển cấp để bước vào kỳ thi vào 10 chuyên thì vô đây like cho mình biết để mình chia sẻ những kinh nghiệm của mình nhé.
Mình chỉ giúp đến mức đủ điểm chứ không lên đến mức thủ khoa hay á khoa đâu nhé, mong mn thông cảm.
Em mới học đến Luỹ thừa (ở trên) thực là em học đến số nguyên tố .-.
Nhìn giống toán 6; 7 hơn là toán 8 nhỉ .
Quá là hữu dụng cho mấy người mù tịt toán như tôi :D tiện thể bạn có thể chia sẻ những tips kiểu như là những cách giúp hứng thú với toán hơn hoặc là nhớ công thức toán 1 cách dễ hơn được không? Làm vậy có thể giúp các bạn đỡ mất gốc toán và thích học toán hơn ☺
tôi chuẩn bị vào 7 nên muốn hỏi bạn có kiến thức lớp 7 ko vậy :)