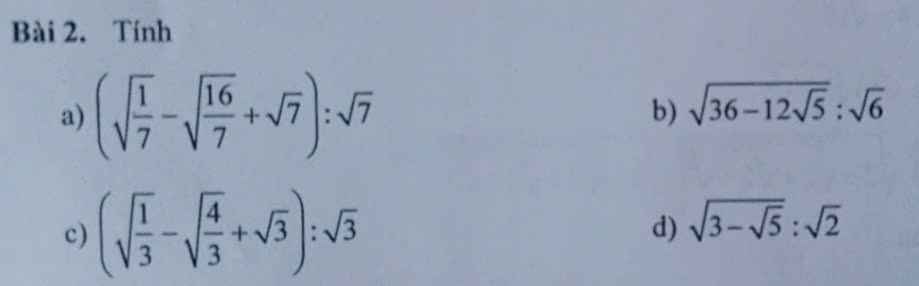a; (\(\sqrt{\dfrac{1}{7}}\) - \(\sqrt{\dfrac{16}{7}}\) + \(\sqrt{7}\)) : \(\sqrt{7}\)
= (\(\dfrac{1}{\sqrt{7}}\) - \(\dfrac{4}{\sqrt{7}}\) + \(\sqrt{7}\)) x \(\dfrac{1}{\sqrt{7}}\)
= \(\dfrac{1}{\sqrt{7}}\) x \(\dfrac{1}{\sqrt{7}}\) - \(\dfrac{4}{\sqrt{7}}\) x \(\dfrac{1}{\sqrt{7}}\) + \(\sqrt{7}\) x \(\dfrac{1}{\sqrt{7}}\)
= \(\dfrac{1}{7}\) - \(\dfrac{4}{7}\) + 1
= - \(\dfrac{3}{7}\) + 1
= - \(\dfrac{3}{7}\) + \(\dfrac{7}{7}\)
= \(\dfrac{4}{7}\)
a: \(\dfrac{\left(\sqrt{\dfrac{1}{7}}-\sqrt{\dfrac{16}{7}}+\sqrt{7}\right)}{\sqrt{7}}\)
\(=\dfrac{\dfrac{\sqrt{7}}{7}-\dfrac{4\sqrt{7}}{7}+\sqrt{7}}{\sqrt{7}}\)
\(=\dfrac{1}{7}-\dfrac{4}{7}+1=1-\dfrac{3}{7}=\dfrac{4}{7}\)
b: \(\sqrt{36-12\sqrt{5}}:\sqrt{6}\)
\(=\sqrt{\dfrac{6\left(6-2\sqrt{5}\right)}{6}}=\sqrt{6-2\sqrt{5}}\)
\(=\sqrt{5-2\cdot\sqrt{5}\cdot1+1}\)
\(=\sqrt{\left(\sqrt{5}-1\right)^2}=\sqrt{5}-1\)
c: \(\left(\sqrt{\dfrac{1}{3}}-\sqrt{\dfrac{4}{3}}+\sqrt{3}\right):\sqrt{3}\)
\(=\left(\dfrac{\sqrt{3}}{3}-\dfrac{2\sqrt{3}}{3}+\sqrt{3}\right):\sqrt{3}\)
\(=\dfrac{1}{3}-\dfrac{2}{3}+1=1-\dfrac{1}{3}=\dfrac{2}{3}\)
d: \(\dfrac{\sqrt{3-\sqrt{5}}}{\sqrt{2}}=\sqrt{\dfrac{3-\sqrt{5}}{2}}=\sqrt{\dfrac{6-2\sqrt{5}}{4}}\)
\(=\sqrt{\dfrac{5-2\cdot\sqrt{5}\cdot1+1}{2^2}}\)
\(=\sqrt{\dfrac{\left(\sqrt{5}-1\right)^2}{2^2}}=\dfrac{\sqrt{5}-1}{2}\)
b; \(\sqrt{36-12\sqrt{5}}\) : \(\sqrt{6}\)
= \(\sqrt{\dfrac{36-12\sqrt{5}}{6}}\)
= \(\sqrt{\dfrac{6.\left(6-2\sqrt{5}\right)}{6}}\)
= \(\sqrt{6-2\sqrt{5}}\)
= \(\sqrt{\sqrt{5}^2-2\sqrt{5}+1^2}\)
= \(\sqrt{\left(\sqrt{5}-1\right)^2}\)
= \(\sqrt{5}\) - 1
c; \(\left(\sqrt{\dfrac{1}{3}}-\sqrt{\dfrac{4}{3}}+\sqrt{3}\right)\) : \(\sqrt{3}\)
= \(\left(\dfrac{1}{\sqrt{3}}-\dfrac{2}{\sqrt{3}}+\dfrac{3}{\sqrt{3}}\right)\) : \(\sqrt{3}\)
= \(\dfrac{1}{\sqrt{3}}\)(1 - 2 + 3) x \(\dfrac{1}{\sqrt{3}}\)
= (\(\dfrac{1}{\sqrt{3}}\) x \(\dfrac{1}{\sqrt{3}}\)).(1 - 2 + 3)
= \(\dfrac{1}{3}\).(- 1 + 3)
= \(\dfrac{1}{3}\). 2
= \(\dfrac{2}{3}\)