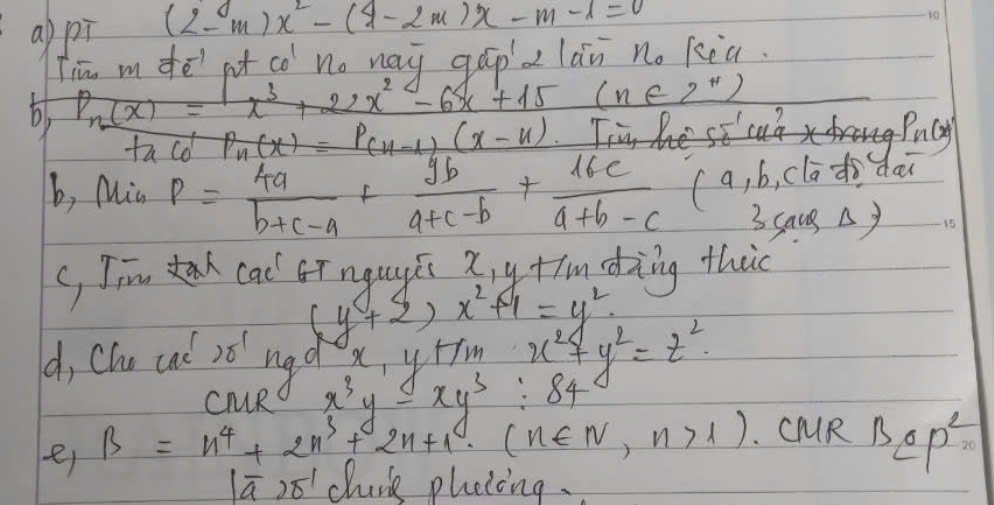b) \(P=\dfrac{4a}{b+c-a}+\dfrac{9b}{a+c-b}+\dfrac{16c}{a+b-c}\)
Đặt \(\left\{{}\begin{matrix}x=b+c-a\\y=a+c-b\\z=a+b-c\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}a=\dfrac{y+z}{2}\\b=\dfrac{x+z}{2}\\c=\dfrac{x+y}{2}\end{matrix}\right.\)
\(\Rightarrow P=\dfrac{2\left(y+z\right)}{x}+\dfrac{9\left(x+z\right)}{2y}+\dfrac{8\left(x+y\right)}{z}\)
\(\Rightarrow P=\left(\dfrac{2y}{x}+\dfrac{9x}{2y}\right)+\left(\dfrac{2z}{x}+\dfrac{8x}{z}\right)+\left(\dfrac{9z}{2y}+\dfrac{8y}{z}\right)\ge6+8+12=26\)
Dấu "=" xảy ra khi và chỉ khi : \(\left\{{}\begin{matrix}\dfrac{2y}{x}=\dfrac{9x}{2y}\\\dfrac{2z}{x}=\dfrac{8x}{z}\\\dfrac{9z}{2y}+\dfrac{8y}{z}\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}\dfrac{x}{y}=\dfrac{2}{3}\\\dfrac{z}{x}=2\\\dfrac{y}{z}=\dfrac{3}{4}\end{matrix}\right.\)
\(\Rightarrow\left(x;y;z\right)=\left(t;\dfrac{3t}{2};2t\right)\left(t>0\right)\)
Vậy \(P\left(min\right)=26\) tại \(\left(x;y;z\right)=\left(t;\dfrac{3t}{2};2t\right)\left(t>0\right)\)
c) \(\left(y+2\right)x^2+1=y^2\)
\(\Leftrightarrow\left(y+2\right)x^2+1-y^2=0\left(1\right)\)
Để \(\left(1\right)\) có nghiệm \(x\in Z\)
\(\Leftrightarrow\left\{{}\begin{matrix}\Delta=4\left(y^2-1\right)\ge0\left(a\right)\\S=0\in Z\left(b\right)\\P=\dfrac{1-y^2}{y+2}\in Z\left(c\right)\end{matrix}\right.\)
\(\left(a\right)\Leftrightarrow y\le-1\cup y\ge1\left(2\right)\)
\(\left(b\right)\Leftrightarrow x=0\left(3\right)\)
\(\left(c\right)\Leftrightarrow P=2-y-\dfrac{3}{y+2}\in Z\)
\(\Leftrightarrow y+2\in U\left(3\right)=\left\{-1;1;-3;3\right\}\)
\(\Leftrightarrow y\in\left\{-3;-1;-5;1\right\}\left(4\right)\) thỏa \(\left(a\right)\)
\(\left(1\right);\left(2\right);\left(3\right);\left(4\right)\Rightarrow\left(x;y\right)=\left(0;1\right);\left(0;-1\right)\)
Vậy với \(\left(x;y\right)=\left(0;1\right);\left(0;-1\right)\) thỏa mãn đề bài
a) \(\left(2-m\right)x^2-\left(1-2m\right)x-m-1=0\left(1\right)\)
\(\Delta=\left(1-2m\right)^2+4\left(m+1\right)\left(2-m\right)\)
\(\Delta=1-4m+4m^2-4m^2+4m+8=9>0\)
\(\Rightarrow\left(1\right)\) luôn có 2 nghiệm phân biệt \(x_1;x_2\)
Theo đề bài ta có :
\(x_1=2x_2\)
\(\Leftrightarrow\dfrac{1-2m+3}{2\left(2-m\right)}=\dfrac{2\left(1-2m-3\right)}{2\left(2-m\right)}\)
\(\Leftrightarrow4-2m=2\left(-2m-2\right)\)
\(\Leftrightarrow4-2m=-4m+8\)
\(\Leftrightarrow2m=4\)
\(\Leftrightarrow m=2\)
Vậy với \(m=2\) phương trình \(\left(1\right)\) có 2 nghiệm thỏa \(x_1=2x_2\)
d.
Nếu \(x;y\) đều ko chia hết cho 3 \(\Rightarrow x^2+y^2\) chia 3 dư 2
\(\Rightarrow z^2\) chia 3 dư 2 (vô lý)
\(\Rightarrow\) Ít nhất 1 trong 2 số x hoặc y chia hết cho 3
\(\Rightarrow xy\) chia hết cho 3 (1)
Nếu x;y đều ko chia hết cho 4 \(\Rightarrow x^2+y^2\) chia 4 dư 2
\(\Rightarrow z^2\) chia 4 dư 2 (vô lý do 1 SCP chia 4 chỉ dư 0 hoặc 1)
\(\Rightarrow\) Trong 2 số x;y phải có ít nhất 1 số chia hết cho 4
\(\Rightarrow xy\) chia hết cho 4 (2)
Do 1 số chính phương chia 7 chỉ có các số dư 0, 1, 2, 4 nên:
- Nếu \(z^2\) chia 7 dư 0 \(\Rightarrow x^2;y^2\) đều chia hết cho 7
\(\Rightarrow x^2-y^2\) chia hết cho 7
- Nếu \(z^2\) chia 7 dư 1 \(\Rightarrow\) trong 2 số \(x^2;y^2\) có 1 số chia hết cho 7 và 1 số chia 7 dư 1
\(\Rightarrow xy\) chia hết cho 7
- Nếu \(z^2\) chia 7 dư 2 \(\Rightarrow x^2;y^2\) đều chia 7 dư 1
\(\Rightarrow x^2-y^2\) chia hết cho 7
- Nếu \(z^2\) chia 7 dư 4 \(\Rightarrow x^2;y^2\) đều chia 7 dư 2
\(\Rightarrow x^2-y^2\) chia hết cho 7
Từ 4 điều trên ta suy ra luôn có \(xy\) chia hết cho 7 hoặc \(x^2-y^2\) chia hết cho 7
\(\Rightarrow xy\left(x^2-y^2\right)\) chia hết cho 7 (3)
Từ (1);(2);(3) \(\Rightarrow xy\left(x^2-y^2\right)\) chia hết \(3.4.7=84\)
e.
Giả sử \(n^4+2n^3+2n+1=m^2\) (1)
Do \(n>1>0\) nên:
\(n^4+2n^3+2n+1=\left(n^2+n-1\right)^2+\left(n^2+4n\right)>\left(n^2+n-1\right)^2\)
\(n^4+2n^3+2n+1=\left(n^2+n+1\right)^2-3n^2< \left(n^2+n+1\right)^2\)
\(\Rightarrow\left(n^2+n-1\right)^2< n^4+2n^3+2n+1< \left(n^2+n+1\right)^2\) (2)
(1);(2) \(\Rightarrow n^4+2n^3+2n+1=\left(n^2+n\right)^2\)
\(\Rightarrow n^2-2n-1=0\) (ko tồn tại n nguyên thỏa mãn)
Vậy điều giả sử là sai hay B ko phải SCP