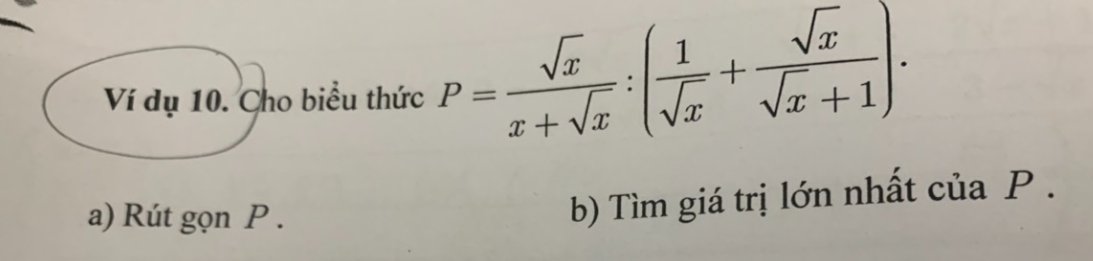b.
\(P=\dfrac{\sqrt{x}}{x+\sqrt{x}+1}=\dfrac{3\sqrt{x}}{3\left(x+\sqrt{x}+1\right)}=\dfrac{x+\sqrt{x}+1-\left(x-2\sqrt{x}+1\right)}{3\left(x+\sqrt{x}+1\right)}\)
\(=\dfrac{1}{3}-\dfrac{\left(\sqrt{x}-1\right)^2}{x+\sqrt{x}+1}\le\dfrac{1}{3}\)
\(P_{max}=\dfrac{1}{3}\) khi \(\sqrt{x}-1=0\Rightarrow x=1\)
a: ĐKXĐ: x>0
\(P=\dfrac{\sqrt{x}}{x+\sqrt{x}}:\left(\dfrac{1}{\sqrt{x}}+\dfrac{\sqrt{x}}{\sqrt{x}+1}\right)\)
\(=\dfrac{\sqrt{x}}{\sqrt{x}\left(\sqrt{x}+1\right)}:\dfrac{\sqrt{x}+1+x}{\sqrt{x}\left(\sqrt{x}+1\right)}\)
\(=\dfrac{\sqrt{x}}{x+\sqrt{x}+1}\)
Câu b rất khó để phân tích nếu như không biết cách làm nháp nhé, mình có để phần đó ở bình luận câu trả lời của thầy Nguyễn Việt Lâm, bạn tham khảo.