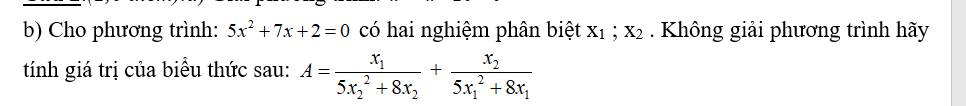Theo Vi-et, ta có:
\(\left\{{}\begin{matrix}x_1+x_2=-\dfrac{b}{a}=-1,4\\x_1x_2=\dfrac{c}{a}=0,4\end{matrix}\right.\)
\(A=\dfrac{x_1}{5x_2^2+8x_2}+\dfrac{x_2}{5x_1^2+8x_1}\)
\(=\dfrac{x_1\left(5x_1^2+8x_1\right)+x_2\left(5x_2^2+8x_2\right)}{\left(5x_1^2+8x_1\right)\left(5x_2^2+8x_2\right)}\)
\(=\dfrac{5\left(x_1^3+x_2^3\right)+8\left(x_1^2+x_2^2\right)}{25\cdot\left(x_1x_2\right)^2+40\cdot x_1x_2\left(x_1+x_2\right)+64\cdot x_1x_2}\)
\(=\dfrac{5\left[\left(x_1+x_2\right)^3-3x_1x_2\left(x_1+x_2\right)\right]+8\left[\left(x_1+x_2\right)^2-2x_1x_2\right]}{25\cdot\left(0,4\right)^2+40\cdot0,4\cdot\left(-1,4\right)+64\cdot\left(0,4\right)}\)
\(=\dfrac{5\left[\left(-1,4\right)^3-3\cdot0,4\cdot\left(-1,4\right)\right]+8\left[\left(-1,4\right)^2-2\cdot0,4\right]}{7,2}\)
\(=\dfrac{3,96}{7,2}=\dfrac{11}{20}\)
Theo Vi-ét ta có: \(\left\{{}\begin{matrix}x_1+x_2=-\dfrac{7}{5}\\x_1\cdot x_2=\dfrac{2}{5}\end{matrix}\right.\)
Theo đề bài ta có: \(A=\dfrac{x_1}{5x_2^2+8x_2}+\dfrac{x_2}{5x_1^2+8x_1}\)
\(=\dfrac{x_1\left(5x_1^2+8x_1\right)+x_2\left(5x_2^2+8x_2\right)}{\left(5x_1^2+8x_1\right)\left(5x_2^2+8x_2\right)}\)
\(=\dfrac{5x_1^3+8x_1^2+5x_2^3+8x_2^2}{25\left(x_1x_2\right)^2+40x_1^2x_2+40x_1x_2^2+64x_1x_2}\)
\(=\dfrac{5\left(x_1^3+x_2^3\right)+8\left(x_1^2+x_2^2\right)}{25\left(x_1x_2\right)^2+40x_1x_2\left(x_1+x_2\right)+64x_1x_2}\)
\(=\dfrac{5\left[\left(x_1+x_2\right)^3-3x_1x_2\left(x_1+x_2\right)\right]+8\left[\left(x_1+x_2\right)^2-2x_1x_2\right]}{25\left(x_1x_2\right)^2+40x_1x_2\left(x_1+x_2\right)+64x_1x_2}\)
\(=\dfrac{5\left[\left(-\dfrac{7}{5}\right)^3-3\cdot\dfrac{2}{5}\cdot\dfrac{-7}{5}\right]+8\left[\left(-\dfrac{7}{5}\right)^2-2\cdot\dfrac{2}{5}\right]}{25\cdot\left(\dfrac{2}{5}\right)^2+40\cdot\dfrac{2}{5}\cdot\dfrac{-7}{5}+64\cdot\dfrac{2}{5}}\)
\(=\dfrac{5\cdot\dfrac{-133}{125}+8\cdot\dfrac{29}{25}}{4-\dfrac{112}{5}+\dfrac{128}{5}}\)
\(=\dfrac{\dfrac{99}{25}}{\dfrac{36}{5}}=\dfrac{11}{20}\)