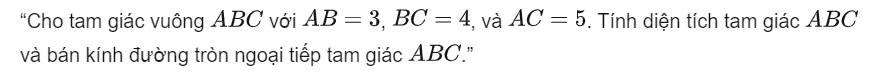Question

Answer 1

S_ABC=3.4=12

R=5/2=2,5

Answer 2

Vì △ABC vuông có AB=3, BC=4, AC=5 → △ABC vuông ở B có AC là c.huyền

⇒ S_ABC=AB.BC=1/2.3.4=6 (đvdd)

 Vì △ABC vuông ở B nên A,B,C cùng thuộc đtron đkinh AC 

⇒ R=\(\dfrac{AC}{2}\)= \(\dfrac{5}{2}=2,5\)

Answer 3

\(S_{ABC}=\dfrac{1}{2}\cdot AB\cdot AC=\dfrac{1}{2}\cdot3\cdot4=6\)

\(AB^2+BC^2=AC^2\left(3^2+4^2=5^2\right)\Rightarrow\Delta ABC\) vuông tại B\(\Rightarrow\) AC là đường kính Đường tròn ngoại tiếp

\(\Rightarrow R=\dfrac{AC}{2}=\dfrac{5}{2}=2.5\)