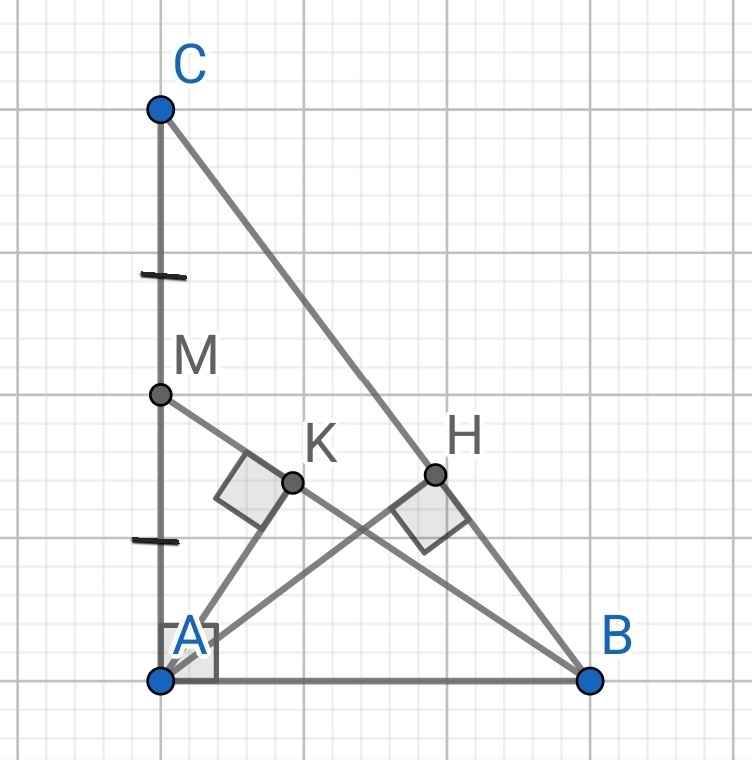
a) BC = BH + CH = 4 + 6 = 10 (cm)
∆ABC vuông tại A có AH là đường cao
⇒ AH² = BH.HC = 4.6 = 24
⇒ AH = 2√6 (cm)
AB² = BH.BC = 4.10 = 40
⇒ AB = 2√10 (cm)
BC² = AB² + AC² (Pytago)
⇒ AC² = BC² - AB²
= 10² - (2√10)²
= 60
⇒ AC = 2√15 (cm)
b) Do M là trung điểm AC (gt)
⇒ AM = AC : 2
= 2√15 : 2
= √15 (cm)
∆AMB vuông tại A
⇒ tanAMB = AB/AM
= 2√10/√15
= 2√6/3
⇒ AMB ≈ 59⁰
c) ∆AMB vuông tại A có AK là đường cao
⇒ AB² = BK.BM (1)
∆ABC vuông tại A có AH là đường cao
⇒ AB² = BH.BC (2)
Từ (1) và (2) ⇒ BK.BM = BH.BC
a AH2=HC*HB
AH2=6*4
AH=√24=2√6
TA CÓ BC=6+4=10
AB^2=BC*HB
AB^2=10*4=40
TA CÓ AC=10*6=60
B AMB=90 ĐỘ
C AB MŨ 2 BẰNG BM NHÂN BK (1)
AB MŨ 2 BẰNG BC NHÂN BH (2)
TỪ 1 VÀ 2 SUY RA .....
