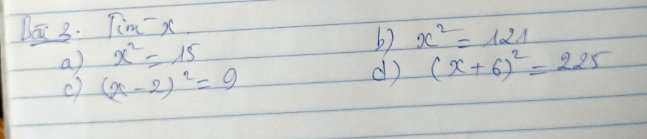a) \(x^2=15\Leftrightarrow x=\pm\sqrt{15}\)
Vậy x = \(\pm\sqrt{15}\)
b) \(x^2=121\Leftrightarrow x=\pm\sqrt{121}=\pm11\)
Vậy x = \(\pm11\)
c) \(\left(x-2\right)^2=9\Leftrightarrow x-2=\pm\sqrt{9}=\pm3\Leftrightarrow\left[{}\begin{matrix}x-2=3\Leftrightarrow x=5\\x-2=-3\Leftrightarrow x=-1\end{matrix}\right.\)
Vậy x ∈ {-1; 5}
d) \(\left(x+6\right)^2=225\Leftrightarrow x+6=\pm\sqrt{225}=\pm15\Leftrightarrow\left[{}\begin{matrix}x+6=15\Leftrightarrow x=9\\x+6=-15\Leftrightarrow x=-21\end{matrix}\right.\)
Vậy x ∈ {-21; 9}
a/ \(x^2=15\Leftrightarrow x=\pm\sqrt{15}\)
b/ \(x^2=121\Leftrightarrow x=\sqrt{121}\Leftrightarrow x=\pm11\)
c/ \(\left(x-2\right)^2=9\Leftrightarrow\left(x-2\right)^2=3^2\Leftrightarrow\left[{}\begin{matrix}x-2=-3\\x-2=3\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=-1\\x=5\end{matrix}\right.\)
d/ \(\left(x+6\right)^2=225\Leftrightarrow\left(x+6\right)^2=15^2\Leftrightarrow\left[{}\begin{matrix}x+6=-15\\x+6=15\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=-21\\x=9\end{matrix}\right.\)
\(a,x^2=15\\ \Leftrightarrow\left[{}\begin{matrix}x=\sqrt{15}\\x=-\sqrt{15}\end{matrix}\right.\)
Vậy \(S=\left\{\sqrt{15};-\sqrt{15}\right\}\)
\(b,x^2=121\\ \Leftrightarrow x^2=11^2\\ \Leftrightarrow\left[{}\begin{matrix}x=11\\x=-11\end{matrix}\right.\)
Vậy \(S=\left\{11;-11\right\}\)
\(c,\left(x-2\right)^2=9\\ \Leftrightarrow\left(x-2\right)^2=3^2\\ \Leftrightarrow x-2=\pm3^2\\ \Leftrightarrow\left[{}\begin{matrix}x-2=3\\x-2=-3\end{matrix}\right.\\ \Leftrightarrow\left[{}\begin{matrix}x=5\\x=-1\end{matrix}\right.\)
Vậy \(S=\left\{-1;5\right\}\)
\(d,\left(x+6\right)^2=225\\ \Leftrightarrow\left(x+6\right)^2=15^2\\ \Leftrightarrow x+6=\pm15\\ \Leftrightarrow\left[{}\begin{matrix}x+6=15\\x+6=-15\end{matrix}\right.\\ \Leftrightarrow\left[{}\begin{matrix}x=9\\x=-21\end{matrix}\right.\)
Vậy \(S=\left\{9;-21\right\}\)
a) \(x^2=15\)
\(\Leftrightarrow x=\pm\sqrt{15}\)
b) \(x^2=121\)
\(\Leftrightarrow x=\pm\sqrt{121}\)
\(\Leftrightarrow x=\pm11\)
c) \(\left(x-2\right)^2=9\)
\(\Leftrightarrow x-2=\sqrt{9}\)
\(\Leftrightarrow x-2=3\)
\(\Leftrightarrow\left[{}\begin{matrix}x-2=-3\\x-2=3\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-1\\x=5\end{matrix}\right.\)
d) \(\left(x+6\right)^2=225\)
\(\Leftrightarrow x+6=\sqrt{225}\)
\(\Leftrightarrow x+6=15\)
\(\Leftrightarrow\left[{}\begin{matrix}x+6=-15\\x+6=15\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-21\\x=9\end{matrix}\right.\)
\(\Leftrightarrow x=9\)
Câu c mik ko nhìn rõ lắm nên mik lm 2 th 0 và 9 nhé
$a)x^2=15$
$\Leftrightarrow x=$\(\pm\)$\sqrt{15}$
Vậy phương trình có tập nghiệm:$S={-\sqrt{15};+\sqrt{15}}$
$b)x^2=121$
$\Leftrightarrow x=$\(\pm\)$\sqrt{121}$
$\Leftrightarrow x=$\(\pm\)$12$
Vậy phương trình có tập nghiệm:$S={$12;-12}$
$c1)(x-2)^2=0$
$\Leftrightarrow x-2=0$
$\Leftrightarrow x=2$
Vậy phương trình có nghiệm $x=2$
$c2)(x-2)^2=9$
$\Leftrightarrow \left[\begin{array}{}
x-2=3\\
x-2=-3
\end{array} \right.$
$\Leftrightarrow\left[\begin{array}{}
x=5\\
x=-1
\end{array} \right.$
Vậy phương trình có tập nghiệm $S={3;-1}$
$d)(x+6)^2=225$
$\Leftrightarrow \left[\begin{array}{}
x+6=15\\
x+6=-15
\end{array} \right.$
$\Leftrightarrow \left[\begin{array}{}
x=9\\
x=-21
\end{array} \right.$
Vậy phương trình có tập nghiệm$S={9;-21}$