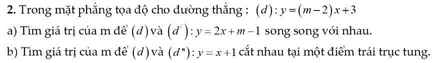a. Hai đường thẳng đã cho song song khi:
\(\left\{{}\begin{matrix}m-2=2\\3\ne m-1\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}m=4\\m\ne4\end{matrix}\right.\)
\(\Rightarrow\) Không tồn tại m để 2 đường thẳng song song
b. Phương trình hoành độ giao điểm d và d'':
\(\left(m-2\right)x+3=x+1\)
\(\Leftrightarrow\left(m-3\right)x=-2\)
- Với \(m=3\Rightarrow\) hai đường thẳng ko cắt nhau (loại)
- Với \(m\ne3\Rightarrow x=-\dfrac{2}{m-3}\)
Để 2 đường thẳng cắt nhau tại 1 điểm nằm bên trái trục tung
\(\Rightarrow-\dfrac{2}{m-3}< 0\Rightarrow m-3>0\Rightarrow m>3\)
Lời giải:
a. Để $(d)\parallel (d')$ thì:
\(\left\{\begin{matrix} m-2=2\\ 3\neq m-1\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} m=4\\ m\neq 4\end{matrix}\right.\) (vô lý)
Vậy không tồn tại $m$ thỏa đề.
b.
PT hoành độ giao điểm:
$(m-2)x+3=x+1$
$\Leftrightarrow x(m-3)+2=0$
$\Leftrightarrow x(m-3)=-2(*)$
Hai đt cắt nhau tại 1 điểm trái trục tung tức là cắt nhau tại điểm có hoành độ âm
$\Leftrightarrow pt (*)$ có nghiệm $x$ âm
$\Leftrightarrow m\neq 3$ và $\frac{-2}{m-3}<0$
$\Leftrightarrow m>3$