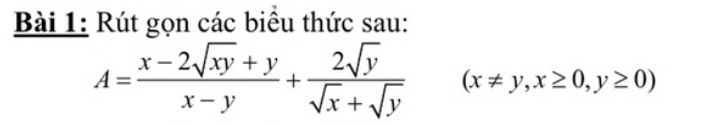Question

Answer 1

\(A=\dfrac{\left(\sqrt{x}-\sqrt{y}\right)^2}{\left(\sqrt{x}-\sqrt{y}\right)\left(\sqrt{x}+\sqrt{y}\right)}+\dfrac{2\sqrt{y}}{\sqrt{x}+\sqrt{y}}\)

\(=\dfrac{\sqrt{x}-\sqrt{y}+2\sqrt{y}}{\sqrt{x}+\sqrt{y}}=\dfrac{\sqrt{x}+\sqrt{y}}{\sqrt{x}+\sqrt{y}}=1\)

Answer 2

\(A=\dfrac{x-2\sqrt{xy}+y}{x-y}+\dfrac{2\sqrt{y}}{\sqrt{x}+\sqrt{y}}\\ =\dfrac{\left(\sqrt{x}-\sqrt{y}\right)^2}{\left(\sqrt{x}-\sqrt{y}\right)\left(\sqrt{x}+\sqrt{y}\right)}+\dfrac{2\sqrt{y}}{\sqrt{x}+\sqrt{y}}\\ =\dfrac{\sqrt{x}-\sqrt{y}}{\sqrt{x}+\sqrt{y}}+\dfrac{2\sqrt{y}}{\sqrt{x}+\sqrt{y}}\\ =\dfrac{\sqrt{x}+\sqrt{y}}{\sqrt{x}+\sqrt{y}}=1\)

Answer 3

\(A=\dfrac{x-2\sqrt{xy}+y}{x-y}+\dfrac{2\sqrt{y}}{\sqrt{x}+\sqrt{y}}\)

\(=\dfrac{\sqrt{x}-\sqrt{y}}{\sqrt{x}+\sqrt{y}}+\dfrac{2\sqrt{y}}{\sqrt{x}+\sqrt{y}}\)

=1