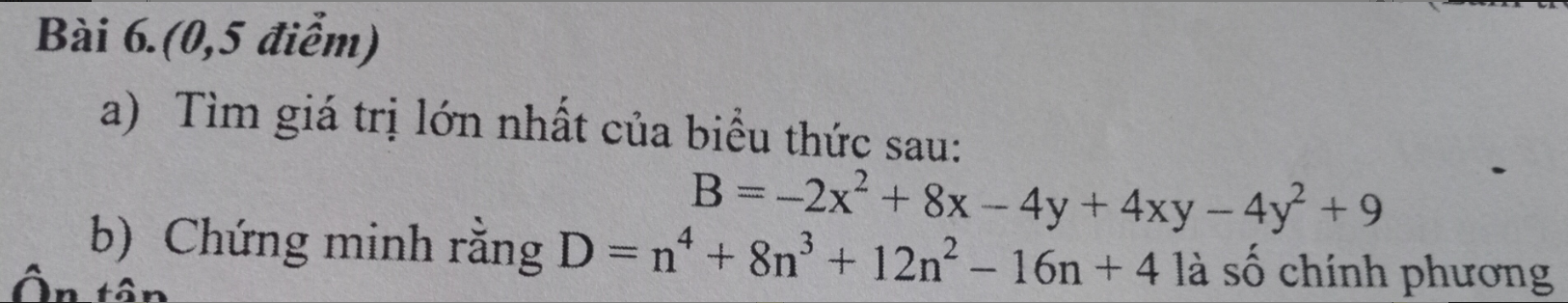a) \(...B=-2\left(x^2+y^2+4-4x+4y-2xy\right)-2\left(y^2-2y+1\right)+8+2+9\)
\(\Rightarrow B=-2\left(x-y-2\right)^2-2\left(y-1\right)^2+19\)
\(\Rightarrow B=-2\left[\left(x-y-2\right)^2+\left(y-1\right)^2\right]+19\le19,\forall x;y\in R\)
Dấu "=" xảy ra khi \(\left\{{}\begin{matrix}x-y-2=0\\y-1=0\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}x=3\\y=1\end{matrix}\right.\)
Vậy \(GTLN\left(B\right)=19\left(tại.x=3;y=1\right)\)
b) \(...D=\left(n^4+8n^3+16n^2\right)-4n^2-16n+4\)
\(\Rightarrow D=\left(n^2+4n\right)^2-4\left(n^2+4n\right)+4\)
\(\Rightarrow D=\left(n^2+4n-2\right)^2\) là số chính phương
\(\Rightarrowđpcm\)