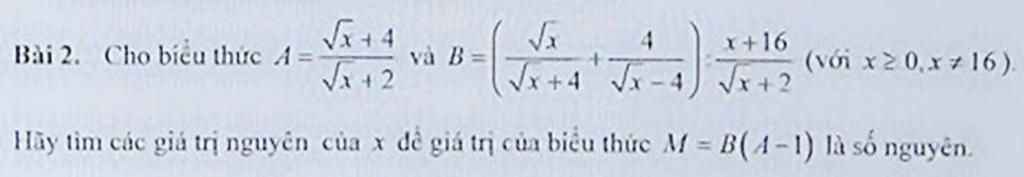Ta có: \(B=\left(\dfrac{\sqrt{x}}{\sqrt{x}+4}+\dfrac{4}{\sqrt{x}-4}\right):\dfrac{x+16}{\sqrt{x}+2}\)
\(=\dfrac{\sqrt{x}\left(\sqrt{x}-4\right)+4\left(\sqrt{x}+4\right)}{\left(\sqrt{x}+4\right)\left(\sqrt{x}-4\right)}\cdot\dfrac{\sqrt{x}+2}{x+16}\)
\(=\dfrac{x-4\sqrt{x}+4\sqrt{x}+16}{\left(\sqrt{x}+4\right)\left(\sqrt{x}-4\right)}\cdot\dfrac{\sqrt{x}+2}{x+16}\)
\(=\dfrac{\sqrt{x}+2}{\left(\sqrt{x}+4\right)\left(\sqrt{x}-4\right)}\)
M=B(A-1)
\(=\dfrac{\sqrt{x}+2}{\left(\sqrt{x}+4\right)\left(\sqrt{x}-4\right)}\cdot\left(\dfrac{\sqrt{x}+4}{\sqrt{x}+2}-1\right)\)
\(=\dfrac{\sqrt{x}+2}{\left(\sqrt{x}+4\right)\left(\sqrt{x}-4\right)}\cdot\dfrac{\sqrt{x}+4-\sqrt{x}-2}{\sqrt{x}+2}=\dfrac{2}{x-16}\)
Để M là số nguyên thì \(2⋮x-16\)
=>\(x-16\in\left\{1;-1;2;-2\right\}\)
=>\(x\in\left\{17;15;18;14\right\}\)