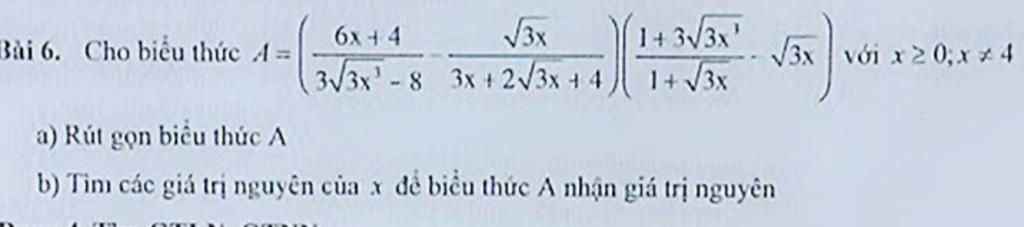a: \(A=\left(\dfrac{6x+4}{3\sqrt{3x^3}-8}-\dfrac{\sqrt{3x}}{3x+2\sqrt{3x}+4}\right)\left(\dfrac{1+3\sqrt{3x^3}}{1+\sqrt{3x}}-\sqrt{3x}\right)\)
\(=\left(\dfrac{6x+4}{\left(\sqrt{3x}\right)^3-2^3}-\dfrac{\sqrt{3x}}{\left(\sqrt{3x}\right)^2+2\cdot\sqrt{3x}+2^2}\right)\left(\dfrac{1+\left(\sqrt{3x}\right)^3}{1+\sqrt{3x}}-\sqrt{3x}\right)\)
\(=\dfrac{6x+4-\sqrt{3x}\left(\sqrt{3x}-2\right)}{\left(\sqrt{3x}-2\right)\left(3x+2\sqrt{3x}+4\right)}\cdot\left(1-\sqrt{3x}+3x-\sqrt{3x}\right)\)
\(=\dfrac{6x+4-3x+2\sqrt{3x}}{\left(\sqrt{3x}-2\right)\left(3x+2\sqrt{3x}+4\right)}\left(1-2\sqrt{3x}+3x\right)\)
\(=\dfrac{3x+2\sqrt{3x}+4}{\left(\sqrt{3x}-2\right)\left(3x+2\sqrt{3x}+4\right)}\cdot\left(\sqrt{3x}-1\right)^2\)
\(=\dfrac{\left(\sqrt{3x}-1\right)^2}{\sqrt{3x}-2}\)
b: Để A nguyên thì \(\left(\sqrt{3x}-1\right)^2⋮\sqrt{3x}-2\)
=>\(3x-2\sqrt{3x}+1⋮\sqrt{3x}-2\)
=>\(\sqrt{3x}\left(\sqrt{3x}-2\right)+1⋮\sqrt{3x}-2\)
=>\(1⋮\sqrt{3x}-2\)
=>\(\sqrt{3x}-2\in\left\{1;-1\right\}\)
=>\(3x\in\left\{9;1\right\}\)
=>\(x\in\left\{3;\dfrac{1}{3}\right\}\)
mà x nguyên
nên x=3