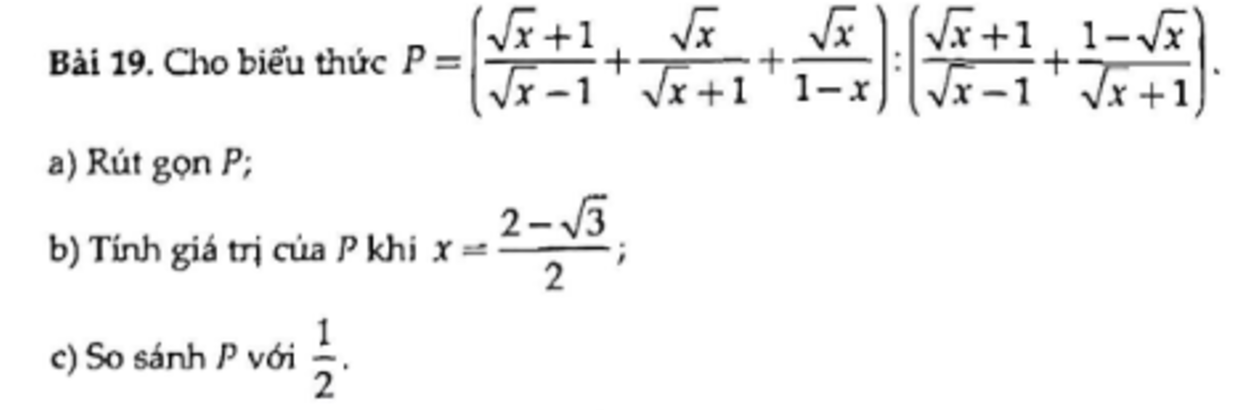a. ĐKXĐ: \(x\ge0;x\ne1\)
\(P=\left(\dfrac{\left(\sqrt{x}+1\right)^2}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}+\dfrac{\sqrt{x}\left(\sqrt{x}-1\right)}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}-\dfrac{\sqrt{x}}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\right):\left(\dfrac{\left(\sqrt{x}+1\right)^2-\left(\sqrt{x}-1\right)^2}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\right)\)
\(=\left(\dfrac{x+2\sqrt{x}+1+x-\sqrt{x}-\sqrt{x}}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\right):\left(\dfrac{4\sqrt{x}}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\right)\)
\(=\dfrac{2x+1}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}.\dfrac{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}{4\sqrt{x}}\)
\(=\dfrac{2x+1}{4\sqrt{x}}\)
b.
\(x=\dfrac{2-\sqrt{3}}{2}=\dfrac{4-2\sqrt{3}}{4}=\left(\dfrac{\sqrt{3}-1}{2}\right)^2\)
\(\Rightarrow\sqrt{x}=\dfrac{\sqrt{3}-1}{2}\)
Khi đó:
\(P=\dfrac{2-\sqrt{3}+1}{4\left(\dfrac{\sqrt{3}-1}{2}\right)}=\dfrac{3-\sqrt{3}}{2\left(\sqrt{3}-1\right)}=\dfrac{\sqrt{3}\left(\sqrt{3}-1\right)}{2\left(\sqrt{3}-1\right)}=\dfrac{\sqrt{3}}{2}\)
c.
\(P=\dfrac{2x+1}{4\sqrt{x}}=\dfrac{\sqrt{x}}{2}+\dfrac{1}{4\sqrt{x}}\ge2\sqrt{\dfrac{\sqrt{x}}{8\sqrt{x}}}=\dfrac{\sqrt{2}}{2}>\dfrac{1}{2}\)
Vậy \(P>\dfrac{1}{2}\)