a) 2x² - 5x + 2 = 0
Δ = (-5)² - 4.2.2 = 15 - 16 = 9 > 0
Phương trình có hai nghiệm phân biệt:
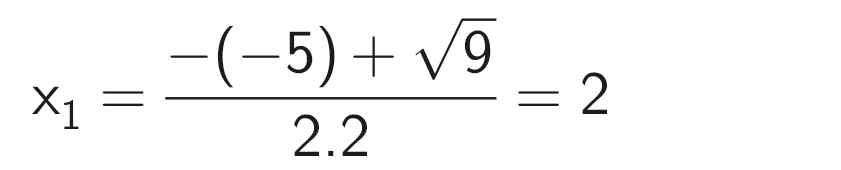
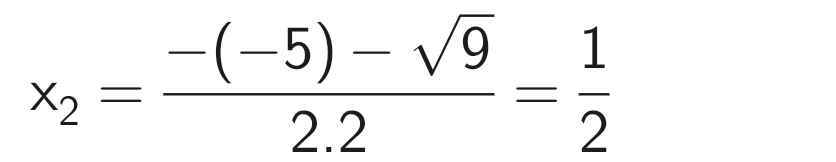
Vậy
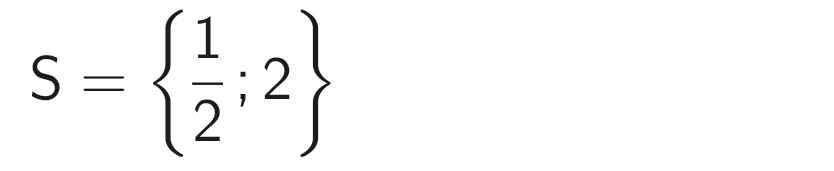
b) -x² + 11x - 30 = 0
x² - 11x + 30 = 0
Δ = (-11)² - 4.1.30 = 1 > 0
Phương trình có hai nghiệm phân biệt:
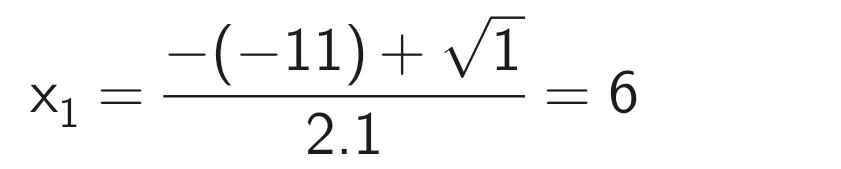
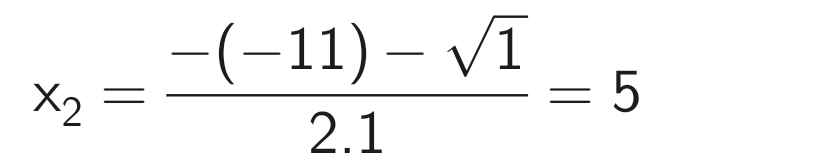
Vậy S = {5; 6}
a: \(2x^2-5x+2=0\)
\(\text{Δ}=\left(-5\right)^2-4\cdot2\cdot2=25-16=9>0\)
Do đó: Phương trình có hai nghiệm phân biệt là:
\(\left[{}\begin{matrix}x=\dfrac{5-\sqrt{9}}{2\cdot2}=\dfrac{5-3}{4}=\dfrac{2}{4}=\dfrac{1}{2}\\x=\dfrac{5+3}{2\cdot2}=\dfrac{8}{4}=2\end{matrix}\right.\)
b: \(-x^2+11x-30=0\)
=>\(x^2-11x+30=0\)
\(\text{Δ}=\left(-11\right)^2-4\cdot1\cdot30=121-120=1>0\)
Do đó: Phương trình có hai nghiệm phân biệt là:
\(\left[{}\begin{matrix}x=\dfrac{11-\sqrt{1}}{2}=\dfrac{11-1}{2}=\dfrac{10}{2}=5\\x=\dfrac{11+1}{2}=\dfrac{12}{2}=6\end{matrix}\right.\)
c:
\(16x^2+24x+9=0\)
\(\text{Δ}=24^2-4\cdot16\cdot9=0\)
Do đó: Phương trình có nghiệm kép là:
\(x=-\dfrac{b}{2a}=\dfrac{-24}{2\cdot16}=-\dfrac{24}{32}=-\dfrac{3}{4}\)
d: \(\dfrac{1}{16}x^2+\dfrac{1}{8}x=\dfrac{1}{2}\)
=>\(\dfrac{1}{16}\left(x^2+2x\right)=\dfrac{1}{16}\cdot8\)
=>\(x^2+2x=8\)
=>\(x^2+2x-8=0\)
\(\text{Δ}=2^2-4\cdot1\cdot\left(-8\right)=4+32=36>0\)
Do đó: Phương trình có hai nghiệm phân biệt là:
\(\left[{}\begin{matrix}x=\dfrac{-2-\sqrt{36}}{2}=\dfrac{-2-6}{2}=-\dfrac{8}{2}=-4\\x=\dfrac{-2+6}{2}=\dfrac{4}{2}=2\end{matrix}\right.\)
e: \(x^2-2\sqrt{3}x+1=0\)
\(\text{Δ}=\left(2\sqrt{3}\right)^2-4\cdot1\cdot1=12-4=8>0\)
Do đó: Phương trình có hai nghiệm phân biệt là:
\(\left[{}\begin{matrix}x=\dfrac{2\sqrt{3}-\sqrt{8}}{2}=\dfrac{2\sqrt{3}-2\sqrt{2}}{2}=\sqrt{3}-\sqrt{2}\\x=\dfrac{2\sqrt{3}+\sqrt{8}}{2}=\sqrt{3}+\sqrt{2}\end{matrix}\right.\)
f: \(\text{Δ}=\left(-3\sqrt{3}\right)^2-4\cdot4\cdot1=27-16=11>0\)
Do đó: Phương trình có hai nghiệm phân biệt là:
\(\left[{}\begin{matrix}x=\dfrac{3\sqrt{3}-\sqrt{11}}{2\cdot4}=\dfrac{3\sqrt{3}-\sqrt{11}}{8}\\x=\dfrac{3\sqrt{3}+\sqrt{11}}{8}\end{matrix}\right.\)
















