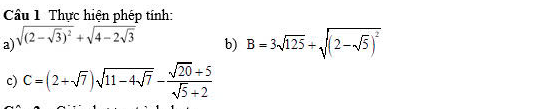a: \(\sqrt{\left(2-\sqrt{3}\right)^2}+\sqrt{4-2\sqrt{3}}\)
\(=\left|2-\sqrt{3}\right|+\sqrt{\left(\sqrt{3}-1\right)^2}\)
\(=2-\sqrt{3}+\sqrt{3}-1=2-1=1\)
b: \(B=3\sqrt{125}+\sqrt{\left(2-\sqrt{5}\right)^2}\)
\(=3\cdot5\sqrt{5}+\sqrt{5}-2=15\sqrt{5}+\sqrt{5}-2=16\sqrt{5}-2\)
c: \(C=\left(2+\sqrt{7}\right)\cdot\sqrt{11-4\sqrt{7}}-\dfrac{\sqrt{20}+5}{\sqrt{5}+2}\)
\(=\left(\sqrt{7}+2\right)\left(\sqrt{7}-2\right)-\dfrac{\sqrt{5}\left(2+\sqrt{5}\right)}{2+\sqrt{5}}\)
\(=7-4-\sqrt{5}=3-\sqrt{5}\)
Đúng 1
Bình luận (0)
