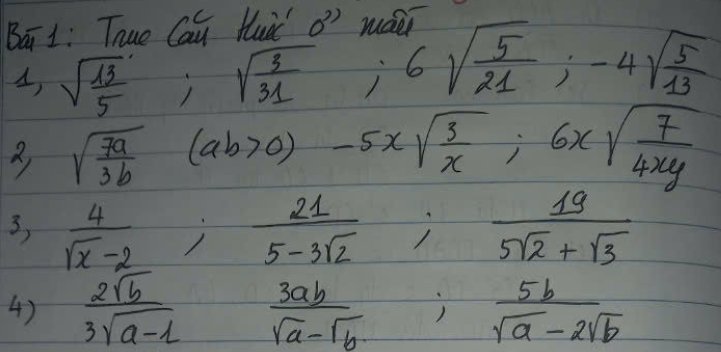1.
\(\sqrt{\dfrac{13}{5}}=\sqrt{\dfrac{13.5}{5.5}}=\dfrac{\sqrt{65}}{5}\)
\(\sqrt{\dfrac{3}{31}}=\dfrac{\sqrt{3}}{\sqrt{31}}=\dfrac{\sqrt{3}.\sqrt{31}}{\sqrt{31}.\sqrt{31}}=\dfrac{\sqrt{93}}{31}\)
\(6\sqrt{\dfrac{5}{21}}=\dfrac{6\sqrt{5}}{\sqrt{21}}=\dfrac{6\sqrt{5}.\sqrt{21}}{\sqrt{21}.\sqrt{21}}=\dfrac{6\sqrt{105}}{21}=\dfrac{2\sqrt{105}}{7}\)
\(-4\sqrt{\dfrac{5}{13}}=\dfrac{-4\sqrt{5}}{\sqrt{13}}=\dfrac{-5\sqrt{5}.\sqrt{13}}{\sqrt{13}.\sqrt{13}}=\dfrac{-4\sqrt{65}}{13}\)
2.
\(\sqrt{\dfrac{7a}{3b}}=\sqrt{\dfrac{7a.3b}{3b.3b}}=\dfrac{\sqrt{21ab}}{3\sqrt{b^2}}=\dfrac{\sqrt{21ab}}{3\left|b\right|}\)
\(-5x\sqrt{\dfrac{3}{x}}=-\dfrac{5x\sqrt{3}}{\sqrt{x}}=-5\sqrt{x}.\sqrt{3}=-5\sqrt{3x}\)
\(6x\sqrt{\dfrac{7}{4xy}}=\dfrac{6x\sqrt{7}}{2\sqrt{xy}}=\dfrac{3x\sqrt{7}.\sqrt{xy}}{\sqrt{xy}.\sqrt{xy}}=\dfrac{3x\sqrt{7xy}}{xy}=\dfrac{3\sqrt{7xy}}{y}\)
3.
\(\dfrac{4}{\sqrt{x}-2}=\dfrac{4\left(\sqrt{x}+2\right)}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}=\dfrac{4\sqrt{x}+8}{x-4}\)
\(\dfrac{21}{5-3\sqrt{2}}=\dfrac{21\left(5+3\sqrt{2}\right)}{\left(5-3\sqrt{2}\right)\left(5+3\sqrt{2}\right)}=\dfrac{21\left(5+3\sqrt{2}\right)}{25-18}=3\left(5+3\sqrt{2}\right)\)
\(\dfrac{19}{5\sqrt{2}+\sqrt{3}}=\dfrac{19\left(5\sqrt{2}-\sqrt{3}\right)}{\left(5\sqrt{2}+\sqrt{3}\right)\left(5\sqrt{2}-\sqrt{3}\right)}=\dfrac{19\left(5\sqrt{2}-\sqrt{3}\right)}{50-3}=\dfrac{19\left(5\sqrt{2}-\sqrt{3}\right)}{47}\)
4.
\(\dfrac{2\sqrt{b}}{3\sqrt{a-1}}=\dfrac{2\sqrt{b}.\sqrt{a-1}}{3\sqrt{a-1}.\sqrt{a-1}}=\dfrac{2\sqrt{b\left(a-1\right)}}{3\left(a-1\right)}\)
\(\dfrac{3ab}{\sqrt{a}-\sqrt{b}}=\dfrac{3ab\left(\sqrt{a}+\sqrt{b}\right)}{\left(\sqrt{a}-\sqrt{b}\right)\left(\sqrt{a}+\sqrt{b}\right)}=\dfrac{3a\left(\sqrt{a}+\sqrt{b}\right)}{a-b}\)
\(\dfrac{5b}{\sqrt{a}-2\sqrt{b}}=\dfrac{5b\left(\sqrt{a}+2\sqrt{b}\right)}{\left(\sqrt{a}-2\sqrt{b}\right)\left(\sqrt{a}+2\sqrt{b}\right)}=\dfrac{5b\left(\sqrt{a}+2\sqrt{b}\right)}{a-4b}\)