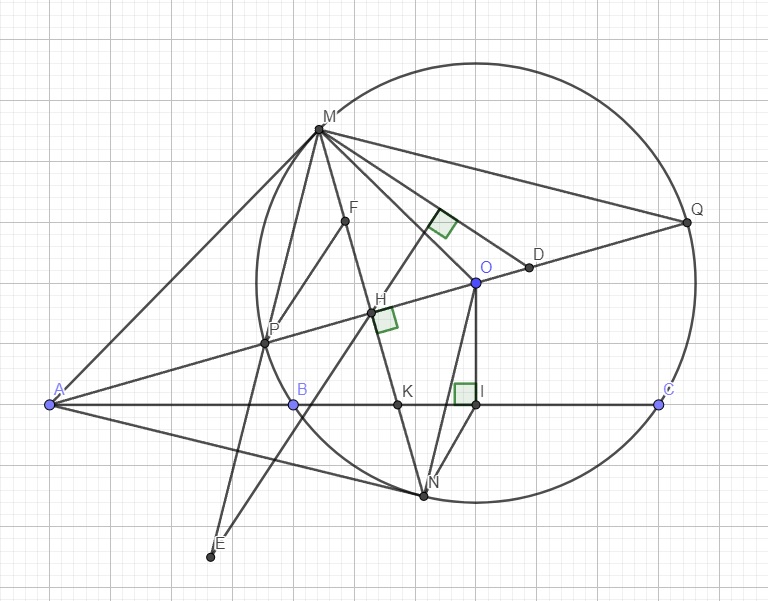
a. Em tự c/m (4 điểm đều thuộc đường tròn đường kính OA).
b.
Gọi giao điểm của MN và AB là K
Theo câu a, AOIN nội tiếp đường tròn đường kính OA \(\Rightarrow\widehat{AON}=\widehat{AIN}\)
Mà \(\left\{{}\begin{matrix}\widehat{AON}+\widehat{ONH}=90^0\\\widehat{ANK}+\widehat{ONH}=90^0\end{matrix}\right.\)
\(\Rightarrow\widehat{AIN}=\widehat{ANK}\) \(\Rightarrow\Delta AKN\sim\Delta ANI\) (chung góc A)
\(\Rightarrow\dfrac{AK}{AN}=\dfrac{AN}{AI}\Rightarrow AK.AI=AN^2\)
Mặt khác theo t/c phương tích (dễ chứng minh), ta có \(AN^2=AB.AC\)
\(\Rightarrow AK.AI=AB.AC\Rightarrow AK=\dfrac{AB.AC}{AI}\)
A, B, C cố định, I là trung điểm BC nên I cố định \(\Rightarrow\dfrac{AB.AC}{AI}=\) hằng số
\(\Rightarrow AK=\) hằng số \(\Rightarrow K\) cố định trên BC
Vậy MN qua K cố định
c.
Gọi F là trung điểm HM (1)
Theo giả thiết D là trung điểm HQ \(\Rightarrow DF\) là đường trung bình tam giác MHQ
\(\Rightarrow DF||MQ\)
Mà \(\widehat{PMQ}=90^0\) (góc nt chắn nửa đường tròn) \(\Rightarrow PM\perp MQ\)
\(\Rightarrow DF\perp PM\)
Lại có \(MH\perp DP\left(gt\right)\)\(\Rightarrow F\) là trực tâm tam giác DMP
\(\Rightarrow PF\perp MD\)
Mà \(EH\perp MD\left(gt\right)\) \(\Rightarrow PF||EH\) (2)
(1);(2) \(\Rightarrow PF\) là đường trung bình tam giác MEH
\(\Rightarrow P\) là trung điểm ME \(\Rightarrow\dfrac{PM}{PE}=1\) ko đổi