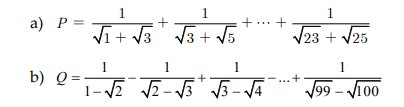a.
\(P=\dfrac{\sqrt{1}-\sqrt{3}}{\left(\sqrt{1}-\sqrt{3}\right)\left(\sqrt{1}+\sqrt{3}\right)}+\dfrac{\sqrt{3}-\sqrt{5}}{\left(\sqrt{3}-\sqrt{5}\right)\left(\sqrt{3}+\sqrt{5}\right)}+...+\dfrac{\sqrt{23}-\sqrt{25}}{\left(\sqrt{23}-\sqrt{25}\right)\left(\sqrt{23}+\sqrt{25}\right)}\)
\(=\dfrac{\sqrt{1}-\sqrt{3}}{1-3}+\dfrac{\sqrt{3}-\sqrt{5}}{3-5}+...+\dfrac{\sqrt{23}-\sqrt{25}}{23-25}\)
\(=\dfrac{\sqrt{1}-\sqrt{3}}{-2}+\dfrac{\sqrt{3}-\sqrt{5}}{-2}+...+\dfrac{\sqrt{23}-\sqrt{25}}{-2}\)
\(=\dfrac{\sqrt{1}-\sqrt{3}+\sqrt{3}-\sqrt{5}+...+\sqrt{23}-\sqrt{25}}{-2}\)
\(=\dfrac{\sqrt{1}-\sqrt{25}}{-2}=\dfrac{1-5}{-2}-2\)
b.
\(Q=\dfrac{1+\sqrt{2}}{\left(1+\sqrt{2}\right)\left(1-\sqrt{2}\right)}-\dfrac{\sqrt{2}+\sqrt{3}}{\left(\sqrt{2}-\sqrt{3}\right)\left(\sqrt{2}+\sqrt{3}\right)}+...+\dfrac{\sqrt{99}+\sqrt{100}}{\left(\sqrt{99}+\sqrt{100}\right)\left(\sqrt{99}-\sqrt{100}\right)}\)
\(=\dfrac{1+\sqrt{2}}{1-2}-\dfrac{\sqrt{2}+\sqrt{3}}{2-3}+\dfrac{\sqrt{3}+\sqrt{4}}{3-4}-\dfrac{\sqrt{4}+\sqrt{5}}{4-5}+...+\dfrac{\sqrt{99}+\sqrt{100}}{99-100}\)
\(=\dfrac{1+\sqrt{2}-\sqrt{2}-\sqrt{3}+\sqrt{3}+\sqrt{4}-\sqrt{4}-\sqrt{5}+...+\sqrt{99}+\sqrt{100}}{-1}\)
\(=\dfrac{1+10}{-1}=-11\)
`a) P = 1/(sqrt{1} + sqrt{3}) + 1/(sqrt{3} + sqrt{5}) + ... + 1/(sqrt{23} + sqrt{25})`
`= (sqrt{3} - 1)/(3 - 1) + (sqrt{5} - sqrt{3})/(5-3) + ... + (sqrt{25} - sqrt{23})/(25-23)`
`= sqrt{3}/2 - 1/2 + sqrt{5}/2 - sqrt{3}/2 + ... + sqrt{25}/2 - sqrt{23}/2`
`= sqrt{25}/2 - 1/2`
`= (5 - 1)/2 `
`= 2`