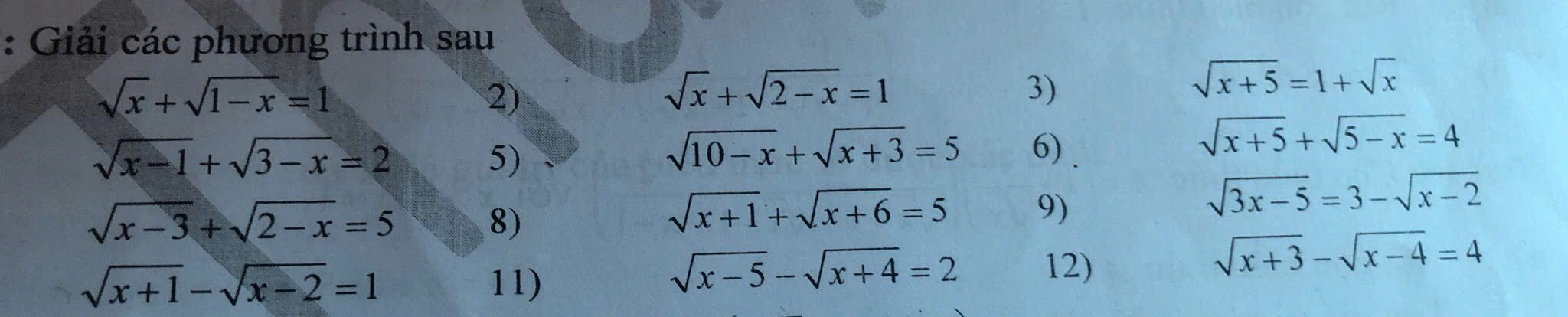1) \(\sqrt{x}+\sqrt{1-x}=1\left(đk:0\le x\le1\right)\)
\(\Leftrightarrow x+1-x+2\sqrt{x\left(1-x\right)}=1\)
\(\Leftrightarrow2\sqrt{x\left(1-x\right)}=0\)
\(\Leftrightarrow4\left[x\left(1-x\right)\right]=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=0\\1-x=0\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}x=0\left(tm\right)\\x=1\left(tm\right)\end{matrix}\right.\)
2) \(\sqrt{x}+\sqrt{2-x}=1\left(đk:0\le x\le2\right)\)
\(\Leftrightarrow x+2-x+2\sqrt{x\left(2-x\right)}=1\)
\(\Leftrightarrow2\sqrt{x\left(2-x\right)}=-1\left(vô.lý\right)\)
\(\Leftrightarrow x\in\varnothing\) (vô nghiệm)
3) \(\sqrt{x+5}=1+\sqrt{x}\left(đk:x\ge0\right)\)
\(\Leftrightarrow\sqrt{x+5}-\sqrt{x}=1\)
\(\Leftrightarrow x+5-x-2\sqrt{x\left(x+5\right)}=1\)
\(\Leftrightarrow2\sqrt{x\left(x+5\right)}=4\)
\(\Leftrightarrow\sqrt{x\left(x+5\right)}=2\)
\(\Leftrightarrow x\left(x+5\right)=4\)
\(\Leftrightarrow x^2+5x-4=0\)
\(\Leftrightarrow x^2+5x+\dfrac{25}{4}-\dfrac{25}{4}-4=0\)
\(\Leftrightarrow\left(x+\dfrac{5}{2}\right)^2-\dfrac{41}{4}=0\)
\(\Leftrightarrow\left(x+\dfrac{5}{2}\right)^2=\dfrac{41}{4}\)
\(\Leftrightarrow\left[{}\begin{matrix}x+\dfrac{5}{2}=\dfrac{\sqrt{41}}{2}\\x+\dfrac{5}{2}=-\dfrac{\sqrt{41}}{2}\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{\sqrt{41}-5}{2}\\x=-\dfrac{\sqrt{41}+5}{2}\left(ktm\right)\end{matrix}\right.\) \(\Leftrightarrow x=\dfrac{\sqrt{41}-5}{2}\)