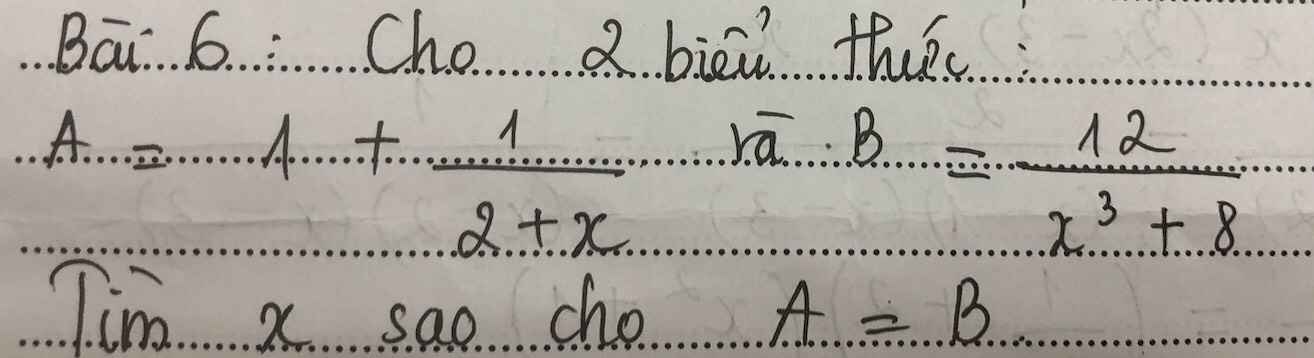ĐKXĐ: x<>-2
\(A=B\)
=>\(1+\dfrac{1}{x+2}=\dfrac{12}{x^3+8}\)
=>\(\dfrac{x+2+1}{x+2}=\dfrac{12}{\left(x+2\right)\left(x^2-2x+4\right)}\)
=>\(\dfrac{x+3}{x+2}=\dfrac{12}{\left(x+2\right)\left(x^2-2x+4\right)}\)
=>\(\left(x+3\right)\left(x^2-2x+4\right)=12\)
=>\(x^3-2x^2+4x+3x^2-6x+12=12\)
=>\(x^3+x^2-2x=0\)
=>x(x+2)(x-1)=0
=>\(\left[{}\begin{matrix}x=0\left(nhận\right)\\x=-2\left(loại\right)\\x=1\left(nhận\right)\end{matrix}\right.\)
`A = B`
`-> 1+1/(2+x) = 12/(x^3+8) (x\ne-2)`
`-> x^3+8 + x^2-2x+4 = 12`
`-> x^3 +x^2 -2x = 0`
`-> x.(x^2+x-2) = 0`
`-> x.(x^2-x+2x-2)=0`
`-> x.(x-1).(x+2) = 0`
-> x = 0 ( TM ) hoặc x = 1 (TM ) hoặc x = -2 (TM )
Vậy `S ={0;1;-2}`