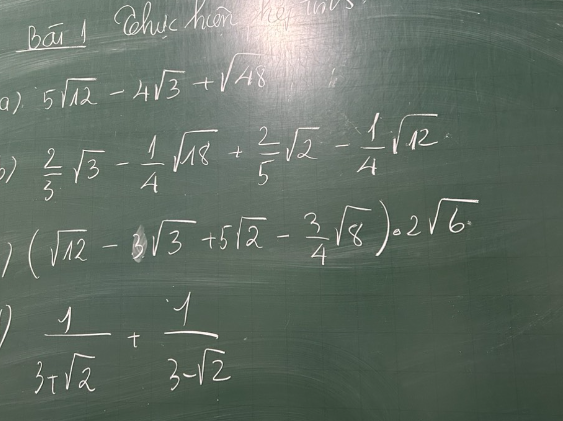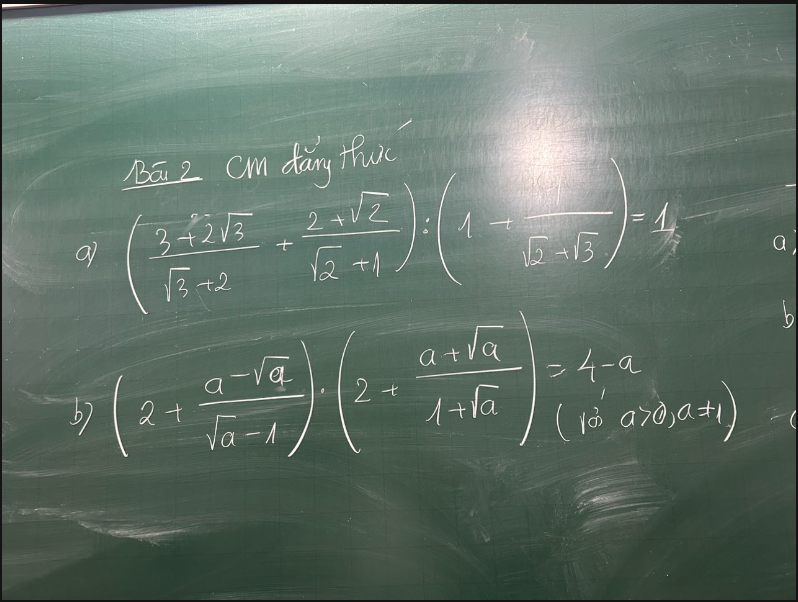Bài 1:
\(\\a,5\sqrt{12}-4\sqrt{3}+\sqrt{48}\\ =5\cdot2\sqrt{3}-4\sqrt{3}+4\sqrt{3}\\ =10\sqrt{3}-4\sqrt{3}+4\sqrt{3}\\ =10\sqrt{3}\\ b,\dfrac{2}{3}\sqrt{3}-\dfrac{1}{4}\sqrt{18}+\dfrac{2}{5}\sqrt{2}-\dfrac{1}{4}\sqrt{12}\\ =\dfrac{2}{3}\sqrt{3}-\dfrac{1}{4}\cdot3\sqrt{2}+\dfrac{2}{5}\sqrt{2}-\dfrac{1}{4}\cdot2\sqrt{3}\\ =\dfrac{2}{3}\sqrt{3}-\dfrac{3}{4}\sqrt{2}+\dfrac{2}{5}\sqrt{2}-\dfrac{1}{2}\sqrt{3}\\ =\left(\dfrac{2}{3}\sqrt{3}-\dfrac{1}{2}\sqrt{3}\right)+\left(-\dfrac{3}{4}\sqrt{2}+\dfrac{2}{5}\sqrt{2}\right)\\ =\dfrac{1}{6}\sqrt{3}+\dfrac{-7}{20}\sqrt{2}\)
\(c,\left(\sqrt{12}-3\sqrt{3}+5\sqrt{2}-\dfrac{3}{4}\sqrt{8}\right)\cdot2\sqrt{6}\\ =\left(2\sqrt{3}-3\sqrt{3}+5\sqrt{2}-\dfrac{3}{4}\cdot2\sqrt{2}\right)\cdot2\sqrt{6}\\ =\left(-\sqrt{3}+5\sqrt{2}-\dfrac{3}{2}\sqrt{2}\right)\cdot2\sqrt{6}\\ =\left(\dfrac{7}{2}\sqrt{2}-\sqrt{3}\right)\cdot2\sqrt{6}\\ =14\sqrt{3}-6\sqrt{2}\\ d,\dfrac{1}{3+\sqrt{2}}+\dfrac{1}{3-\sqrt{2}}\\ =\dfrac{3-\sqrt{2}+3+\sqrt{2}}{\left(3+\sqrt{2}\right)\left(3-\sqrt{2}\right)}\\ =\dfrac{6}{3^2-\left(\sqrt{2}\right)^2}\\ =\dfrac{6}{9-2}\\ =\dfrac{6}{7}\)
Bài 2:
a: \(\left(\dfrac{3+2\sqrt{3}}{\sqrt{3}+2}+\dfrac{2+\sqrt{2}}{\sqrt{2}+1}\right):\left(1+\dfrac{1}{\sqrt{2}+\sqrt{3}}\right)\)
\(=\left(\dfrac{\sqrt{3}\left(2+\sqrt{3}\right)}{2+\sqrt{3}}+\dfrac{\sqrt{2}\left(\sqrt{2}+1\right)}{\sqrt[]{2}+1}\right):\left(1+\dfrac{\sqrt{3}-\sqrt{2}}{3-2}\right)\)
\(=\dfrac{\left(\sqrt{3}+\sqrt{2}\right)}{1+\sqrt{3}-\sqrt{2}}\)
b: \(\left(2+\dfrac{a-\sqrt{a}}{\sqrt{a}-1}\right)\left(2+\dfrac{a+\sqrt{a}}{1+\sqrt{a}}\right)\)
\(=\left(2+\dfrac{\sqrt{a}\left(\sqrt{a}-1\right)}{\sqrt{a}-1}\right)\left(2+\dfrac{\sqrt{a}\left(\sqrt{a}+1\right)}{\sqrt{a}+1}\right)\)
\(=\left(2+\sqrt{a}\right)\left(2+\sqrt{a}\right)=a+4\sqrt{a}+4\)