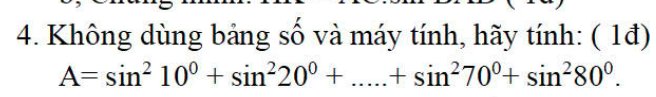\(A=sin^210^o+sin^220^o+...+sin^270^o+sin^280^o\)
\(A=\left(sin^280^o+sin^210^o\right)+\left(sin^270^o+sin^220^o\right)+\left(sin^260^o+sin^230^o\right)+\left(sin^250^o+sin40^o\right)\)\(A=\left(cos^280^o+sin^280^o\right)+\left(cos^270^o+sin^270^o\right)+\left(cos^260^o+sin^260^o\right)+\left(cos^250^o+sin^250^o\right)\)\(A=1+1+1+1=4\)
Ta có : \(sin^210^o=cos^280^o\) \(\left(10^o=90^o-80^o\right)\)
\(sin^220^o=cos^270^o\) \(\left(20^o=90^o-70^o\right)\)
\(.....\)
\(\Rightarrow2A=sin^210^o+cos^210^o+sin^220^o+cos^220^o+...+sin^280^o+cos^280^o\)\(\Rightarrow2A=1+1+...+1\)\(\Rightarrow2A=9\Rightarrow A=\dfrac{9}{2}=4,5\)