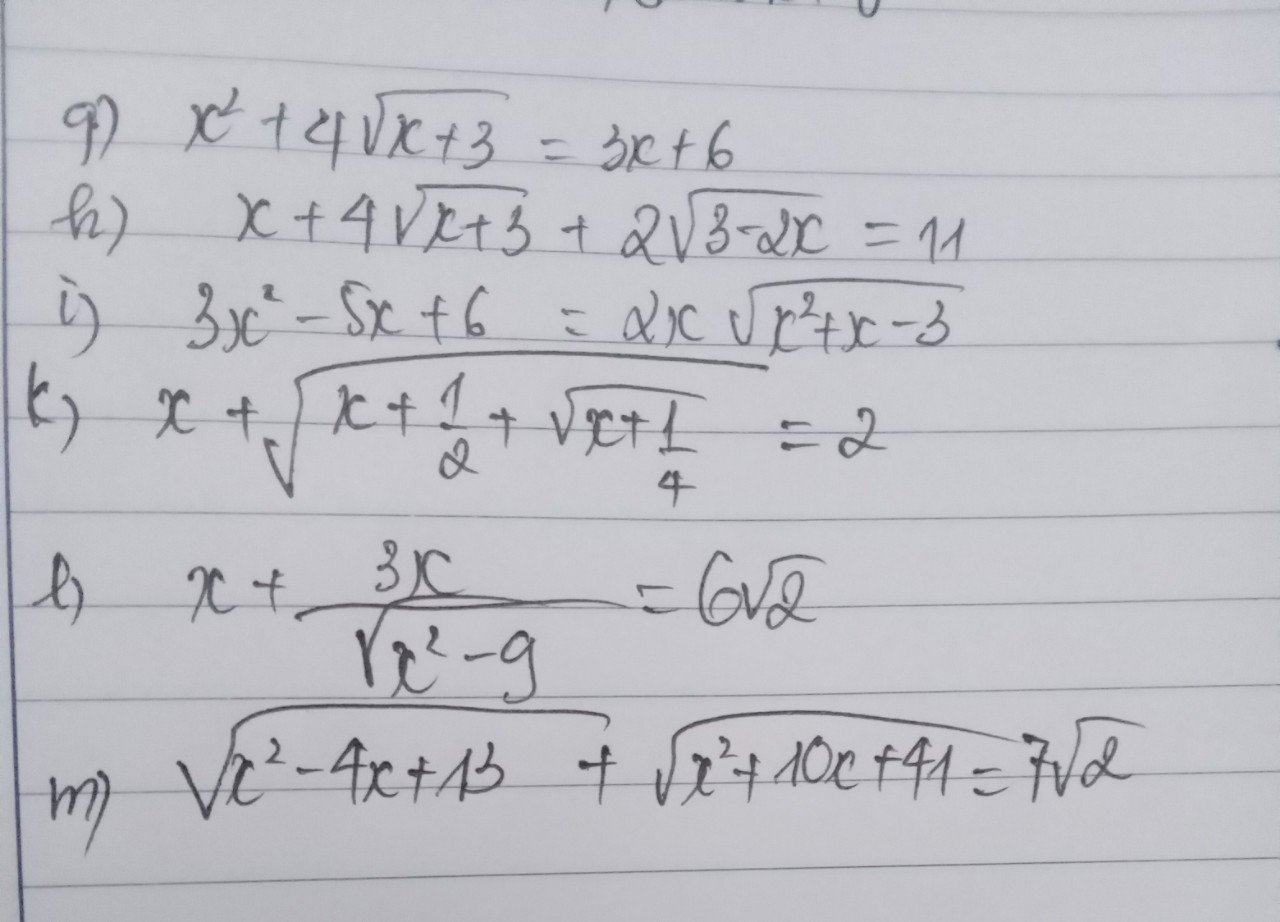1.
ĐKXĐ: \(x\ge-3\)
\(\Leftrightarrow x^2-2x+1-\left(x+3-4\sqrt{x+3}+4\right)=0\)
\(\Leftrightarrow\left(x-1\right)^2-\left(\sqrt{x+3}-2\right)^2=0\)
\(\Leftrightarrow\left(x+1-\sqrt{x+3}\right)\left(x-3+\sqrt{x+3}\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}\sqrt{x+3}=-x-1\\\sqrt{x+3}=3-x\end{matrix}\right.\)
Th1:
\(\sqrt{x+3}=-x-1\)
\(\Leftrightarrow\left\{{}\begin{matrix}-x-1\ge0\\x+3=\left(-x-1\right)^2\end{matrix}\right.\)
\(\Leftrightarrow...\)
TH2: tương tự
2.
ĐKXĐ: \(-3\le x\le\dfrac{3}{2}\)
\(\Leftrightarrow-x-4\sqrt{x+3}-2\sqrt{3-2x}+11=0\)
\(\Leftrightarrow\left(x+3-4\sqrt{x+3}+4\right)+\left(3-2x-2\sqrt{3-2x}+1\right)=0\)
\(\Leftrightarrow\left(\sqrt{x+3}-2\right)^2+\left(\sqrt{3-2x}-1\right)^2=0\)
\(\Leftrightarrow\left\{{}\begin{matrix}\left(\sqrt{x+3}-2\right)^2=0\\\left(\sqrt{3-2x}-1\right)^2=0\end{matrix}\right.\)
\(\Rightarrow x=1\)
3.
\(\Leftrightarrow x^2-6x+9+\left(x^2+x-3-2x\sqrt{x^2+x-3}+x^2\right)=0\)
\(\Leftrightarrow\left(x-3\right)^2+\left(\sqrt{x^2+x-3}-x\right)^2=0\)
\(\Leftrightarrow\left\{{}\begin{matrix}\left(x-3\right)^2=0\\\left(\sqrt{x^2+x-3}-x\right)^2=0\end{matrix}\right.\)
\(\Rightarrow x=3\)
4.
ĐKXĐ: \(x\ge-\dfrac{1}{4}\)
\(\Leftrightarrow2x+\sqrt{4x+2+2\sqrt{4x+1}}=8\)
\(\Leftrightarrow2x+\sqrt{4x+1+2\sqrt{4x+1}+1}=8\)
\(\Leftrightarrow2x+\sqrt{\left(\sqrt{4x+1}+1\right)^2}=8\)
\(\Leftrightarrow2x+\sqrt{4x+1}+1=8\)
\(\Leftrightarrow\sqrt{4x+1}=7-2x\)
\(\Leftrightarrow\left\{{}\begin{matrix}7-2x\ge0\\4x+1=\left(7-2x\right)^2\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x\le\dfrac{7}{2}\\4x^2-32x+48=0\end{matrix}\right.\)
\(\Rightarrow x=2\)
5.
ĐKXĐ: \(\left[{}\begin{matrix}x>3\\x< -3\end{matrix}\right.\)
- Với \(x\le0\Rightarrow x\left(1+\dfrac{3}{\sqrt{x^2-9}}\right)\le0< 6\sqrt{2}\) nên pt vô nghiệm
- Với \(x>0\) bình phương 2 vế:
\(\Rightarrow x^2+\dfrac{9x^2}{x^2-9}+\dfrac{6x^2}{\sqrt{x^2-9}}=72\)
\(\Leftrightarrow\dfrac{x^4}{x^2-9}+\dfrac{6x^2}{\sqrt{x^2-9}}-72=0\)
Đặt \(\dfrac{x^2}{\sqrt{x^2-9}}=t>0\)
\(\Rightarrow t^2+6t-72=0\Rightarrow\left[{}\begin{matrix}t=6\\t=-12\left(loại\right)\end{matrix}\right.\)
\(\Rightarrow\dfrac{x^2}{\sqrt{x^2-9}}=6\)
\(\Rightarrow x^2=6\sqrt{x^2-9}\)
\(\Leftrightarrow x^2-9-6\sqrt{x^2-9}+9=0\)
\(\Leftrightarrow\left(\sqrt{x^2-9}-3\right)^2=0\)
\(\Leftrightarrow x^2=18\)
\(\Rightarrow x=3\sqrt{2}\)
6.
\(\Leftrightarrow\sqrt{\left(x-2\right)^2+9}+\sqrt{\left(x+5\right)^2+16}=7\sqrt{2}\)
\(\Leftrightarrow\sqrt{\left(2-x\right)^2+3^2}+\sqrt{\left(x+5\right)^2+4^2}=7\sqrt{2}\)
Áp dụng BĐT Minkowski:
\(VT\ge\sqrt{\left(2-x+x+5\right)^2+\left(3+4\right)^2}=7\sqrt{2}\)
Dấu "=" xảy ra khi và chỉ khi:
\(3\left(x+5\right)=4\left(2-x\right)\)
\(\Rightarrow x=-1\)