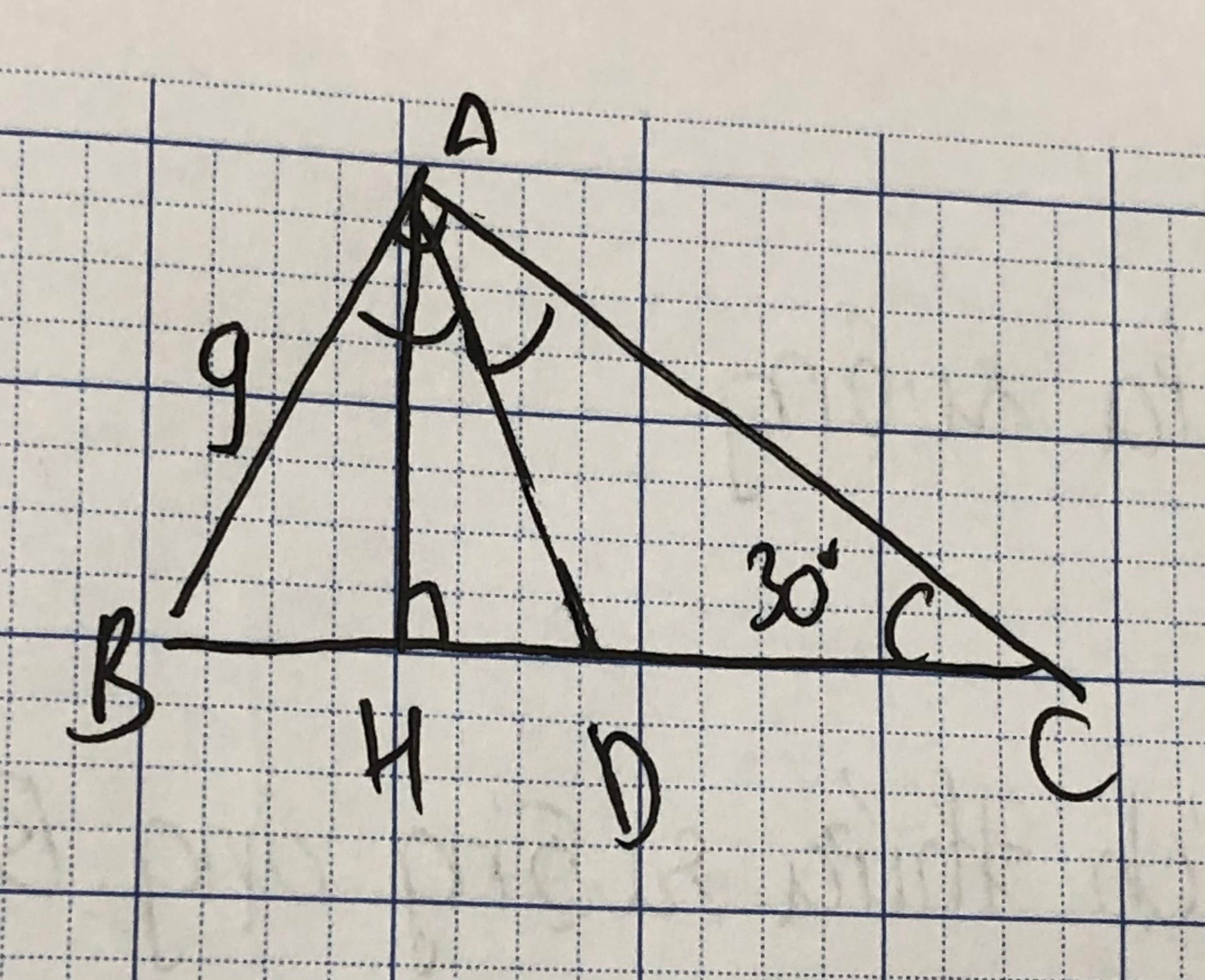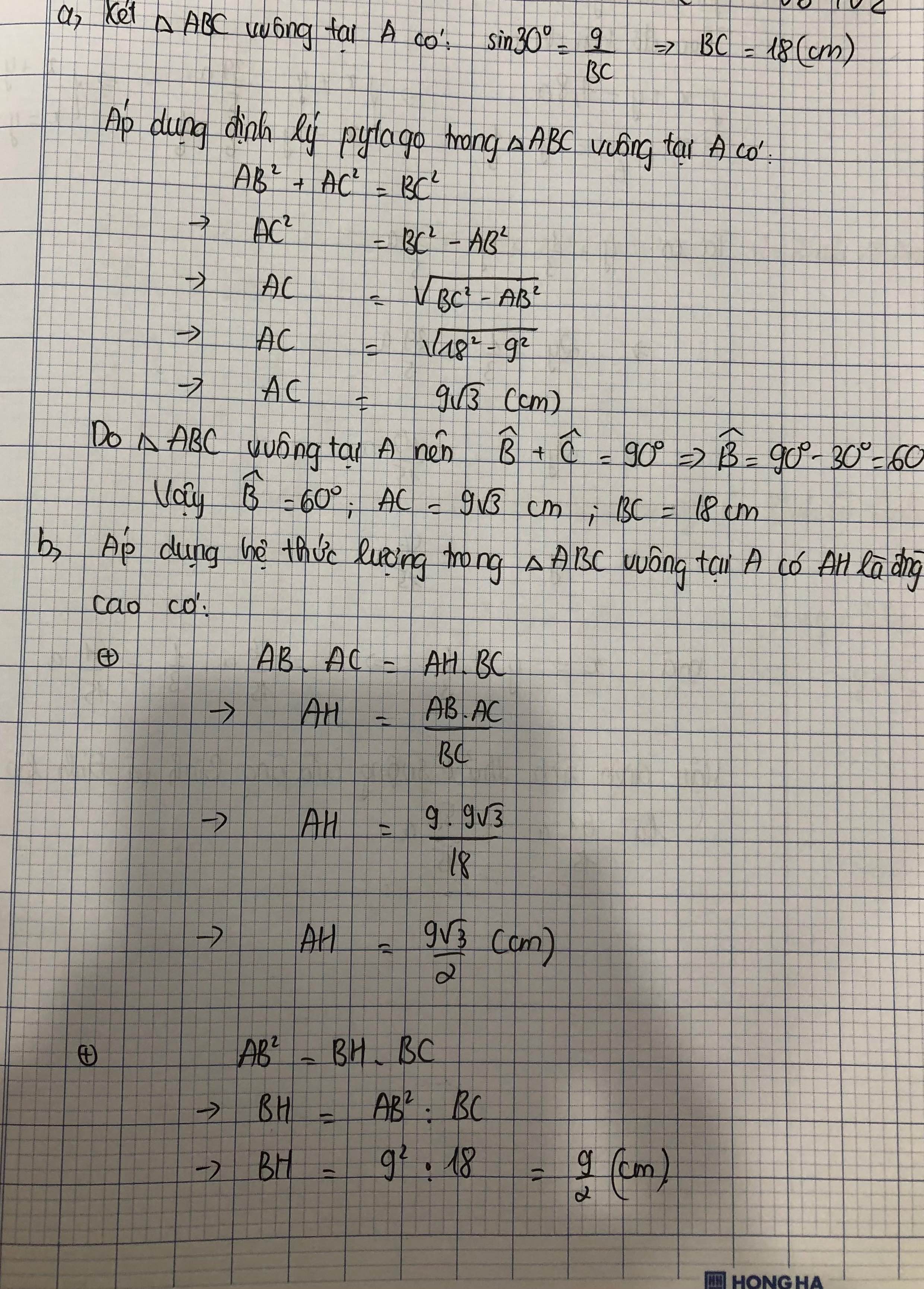1: ΔABC vuông tại A
=>\(\widehat{ABC}+\widehat{ACB}=90^0\)
=>\(\widehat{ABC}=90^0-30^0=60^0\)
Xét ΔABC vuông tại A có \(sinC=\dfrac{AB}{BC}\)
=>\(\dfrac{9}{BC}=sin30=\dfrac{1}{2}\)
=>\(BC=9\cdot2=18\left(cm\right)\)
ΔABC vuông tại A
=>\(AB^2+AC^2=BC^2\)
=>\(AC=\sqrt{18^2-9^2}=9\sqrt{3}\left(cm\right)\)
2: Xét ΔABC vuông tại A có AH là đường cao
nên \(AH\cdot BC=AB\cdot AC\)
=>\(AH\cdot18=9\cdot9\sqrt{3}=81\sqrt{3}\)
=>\(AH=\dfrac{81\sqrt{3}}{18}=\dfrac{9\sqrt{3}}{2}\left(cm\right)\)
Xét ΔABC vuông tại A có AH là đường cao
nên \(BH\cdot BC=BA^2\)
=>\(BH\cdot18=9^2=81\)
=>BH=81/18=4,5(cm)
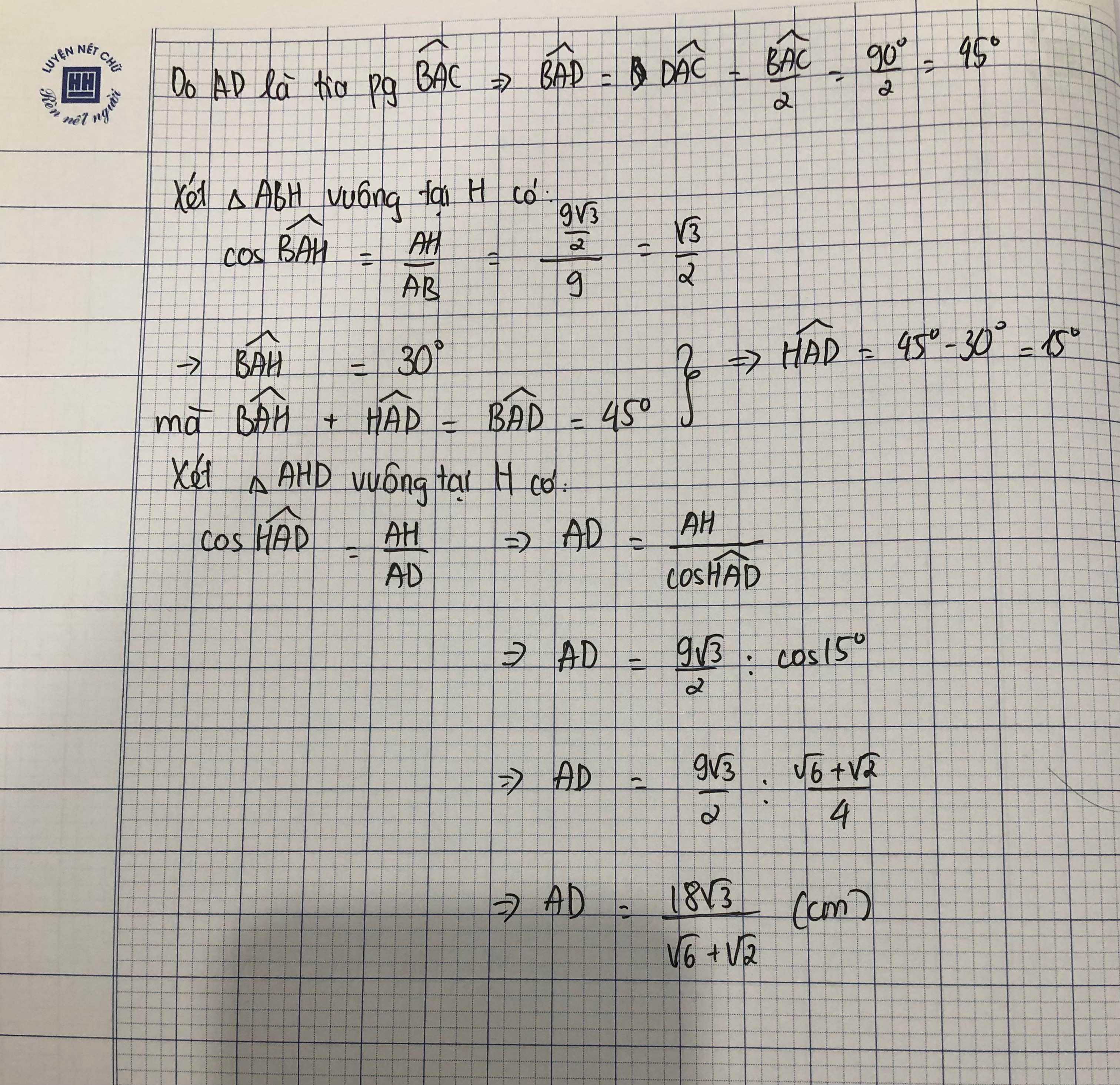
3: Xét ΔBAC có AD là phân giác
nên \(AD=\dfrac{2\cdot AB\cdot AC}{AB+AC}\cdot cos\left(\dfrac{BAC}{2}\right)=\dfrac{2\cdot9\cdot9\sqrt{3}}{9+9\sqrt{3}}\cdot\dfrac{\sqrt{2}}{2}\)
\(=\dfrac{81\sqrt{6}}{9+9\sqrt{3}}=\dfrac{9\sqrt{6}}{\sqrt{3}+1}=\dfrac{9\sqrt{6}\left(\sqrt{3}-1\right)}{2}=\dfrac{27\sqrt{2}-9\sqrt{6}}{2}\left(cm\right)\)