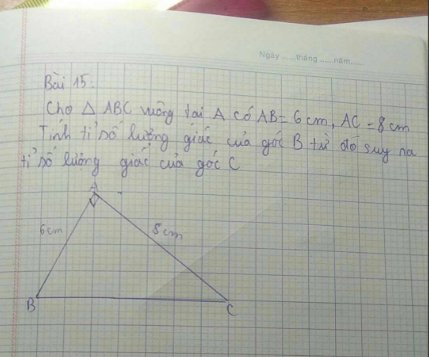
ΔABC vuông tại A
=>\(AB^2+AC^2=BC^2\)
=>\(BC=\sqrt{6^2+8^2}=10\left(cm\right)\)
Xét ΔABC vuông tại A có
\(sinB=cosC=\dfrac{AC}{BC}=\dfrac{8}{10}=\dfrac{4}{5}\)
\(cosB=sinC=\dfrac{AB}{BC}=\dfrac{6}{10}=\dfrac{3}{5}\)
\(tanB=cotC=\dfrac{AC}{AB}=\dfrac{8}{6}=\dfrac{4}{3}\)
\(cotB=tanC=\dfrac{AB}{AC}=\dfrac{6}{8}=\dfrac{3}{4}\)
$#flo$
Xét Δ`ABC` vuông tại A
`=> AB^2 + AC^2 = BC^2`
`=> 6^2 + 8^2 = BC^2`
`=> BC^2= 100`
`=> BC = 10`
Áp dụng hệ định lượng cho Δ`ABC` vuông tại A
\(\sin B=\dfrac{AC}{BC}=\dfrac{8}{10}=\dfrac{4}{5}\)
\(\cos B=\dfrac{AB}{BC}=\dfrac{6}{10}=\dfrac{3}{5}\)
\(\tan B=\dfrac{AC}{AB}=\dfrac{8}{6}=\dfrac{4}{3}\)
\(\cot B=\dfrac{AB}{AC}=\dfrac{6}{8}=\dfrac{3}{4}\)
Theo t/c của ts lượng giác có :
\(\sin B=\cos C=\dfrac{4}{5}\)
\(\cos B=\sin C=\dfrac{3}{5}\)
\(\tan B=\cot C=\dfrac{4}{3}\)
\(\cot B=\tan C=\dfrac{5}{4}\)