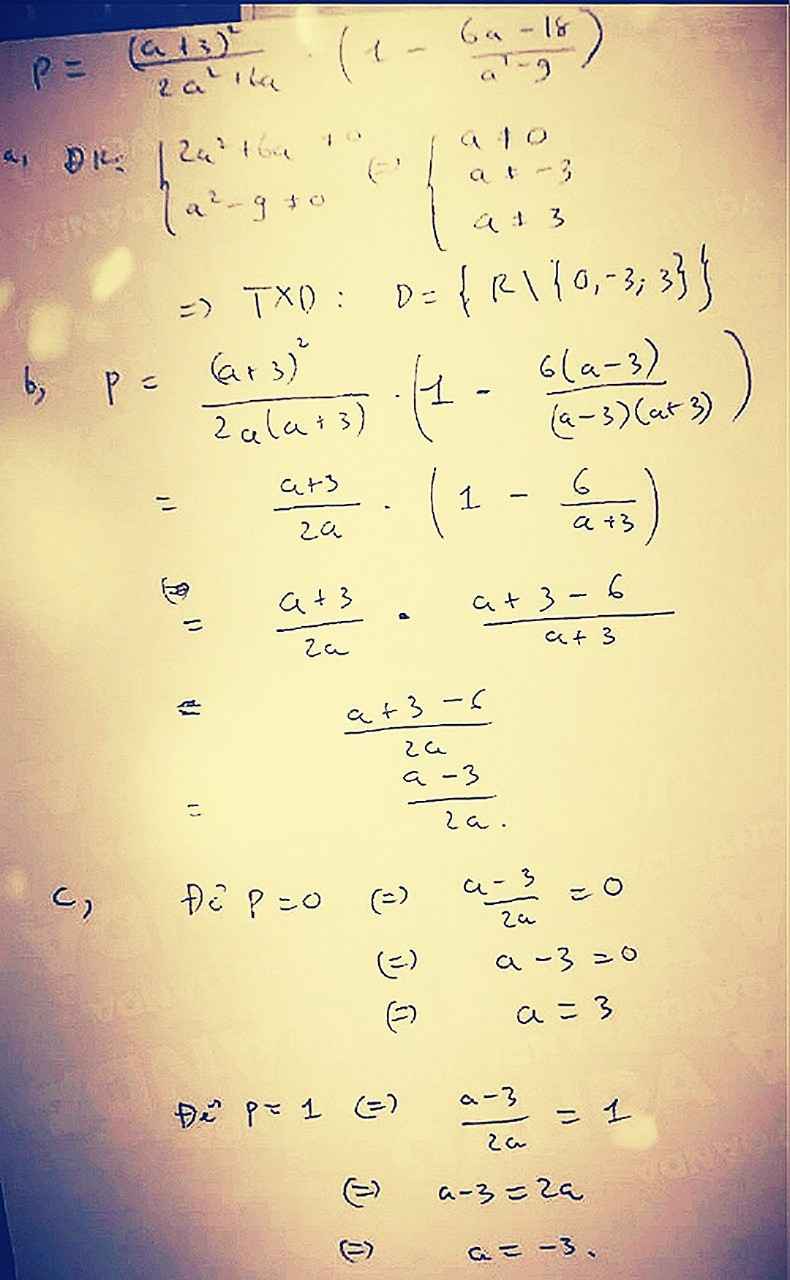a. ĐKXĐ: \(\left\{{}\begin{matrix}2a^2+6a\ne0\\a^2-9\ne0\end{matrix}\right.\Leftrightarrow a\ne0;a\ne\pm3\)
\(b.P=\dfrac{\left(a+3\right)^2}{2a^2+6a}\cdot\left(1-\dfrac{6a-18}{a^2-9}\right)\\ =\dfrac{\left(a+3\right)^2}{2a\left(a+3\right)}\cdot\left[1-\dfrac{6\left(a-3\right)}{\left(a+3\right)\left(a-3\right)}\right]\\ =\dfrac{a+3}{2a}\cdot\left(1-\dfrac{6}{a+3}\right)\\ =\dfrac{a+3}{2a}\cdot\dfrac{a+3-6}{a+3}\\ =\dfrac{a+3}{2a}\cdot\dfrac{a-3}{a+3}\\ =\dfrac{a-3}{2a}\)
c. \(P=0=>\dfrac{a-3}{2a}=0=>a-3=0=>a=3\left(ktm\right)\)
\(P=1=>\dfrac{a-3}{2a}=1=>a-3=2a\\ =>2a-a=3=>a=3\left(ktm\right)\)
Đúng 2
Bình luận (0)
