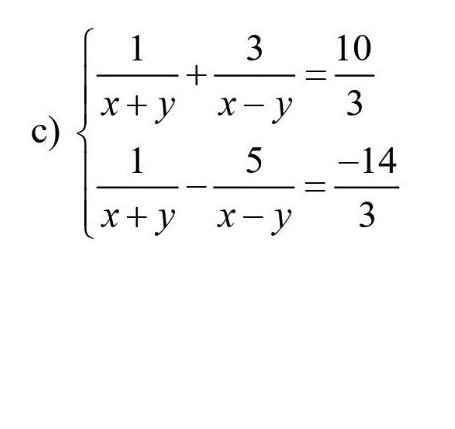\(\left\{{}\begin{matrix}\dfrac{1}{x+y}+\dfrac{3}{x-y}=\dfrac{10}{3}\\\dfrac{1}{x+y}-\dfrac{5}{x-y}=\dfrac{-14}{3}\end{matrix}\right.\)
Đặt \(a=\dfrac{1}{x+y};b=\dfrac{1}{x-y}\)
\(\Rightarrow\left\{{}\begin{matrix}a+3b=\dfrac{10}{3}\\a-5b=-\dfrac{14}{3}\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}a+3b=\dfrac{10}{3}\\8b=8\end{matrix}\right.\\ \Rightarrow\left\{{}\begin{matrix}a=\dfrac{1}{3}\\b=1\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}x+y=3\\x-y=1\end{matrix}\right.\\ \Rightarrow\left\{{}\begin{matrix}2x=4\\x-y=1\end{matrix}\right.\\ \Rightarrow\left\{{}\begin{matrix}x=2\\y=1\end{matrix}\right.\)
Vậy hệ phương trình có nghiệm x = 2 và y = 1
\(\text{Đặt }\dfrac{1}{x+y}=a;\dfrac{1}{x-y}=b\)
\(\left\{{}\begin{matrix}a+3b=\dfrac{10}{3}\\a-5b=\dfrac{-14}{3}\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}8b=8\\a-5b=\dfrac{-14}{3}\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}b=1\\a=\dfrac{1}{3}\end{matrix}\right.\)
\(\text{Vì }\dfrac{1}{x+y}=a;\dfrac{1}{x-y}=b\)
\(\Leftrightarrow\left\{{}\begin{matrix}\dfrac{1}{x+y}=\dfrac{1}{3}\\\dfrac{1}{x-y}=1\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x+y=3\\x-y=1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}2y=2\\x-y=1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=1\\x=2\end{matrix}\right.\)
\(\text{Vậy hệ phương trình đã cho có nghiệm duy nhất là }\left(2;1\right)\)