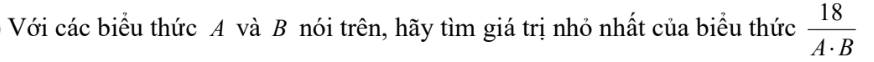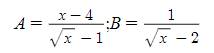ĐKXĐ: \(\left\{{}\begin{matrix}x>=0\\x\notin\left\{1;4\right\}\end{matrix}\right.\)
Đặt\(P=\dfrac{18}{A\cdot B}=18:\left(\dfrac{x-4}{\sqrt{x}-1}\cdot\dfrac{1}{\sqrt{x}-2}\right)\)
\(=18:\left(\dfrac{\sqrt{x}+2}{\sqrt{x}-1}\right)=\dfrac{18\left(\sqrt{x}-1\right)}{\sqrt{x}+2}\)
\(=\dfrac{18\left(\sqrt{x}+2-3\right)}{\sqrt{x}+2}=18-\dfrac{54}{\sqrt{x}+2}\)
Để P nhỏ nhất thì \(\dfrac{54}{\sqrt{x}+2}\) lớn nhất
mà \(\dfrac{54}{\sqrt{x}+2}< =\dfrac{54}{2}=27\forall x\) thỏa mãn ĐKXĐ
nên dấu '=' xảy ra khi x=0
Vậy: \(P_{min}=18-\dfrac{54}{2}=18-27=-9\)
\(AB=\dfrac{x-4}{\sqrt{x}-1}.\dfrac{1}{\sqrt{x}-2}=\dfrac{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}{\left(\sqrt{x}-1\right)\left(\sqrt{x}-2\right)}=\dfrac{\sqrt{x}+2}{\sqrt{x}-1}\)
Đặt \(P=\dfrac{18}{AB}=\dfrac{18\left(\sqrt{x}-1\right)}{\sqrt{x}+2}=18\left(\dfrac{\sqrt{x}+2-3}{\sqrt{x}+2}\right)=18\left(1-\dfrac{3}{\sqrt{x}+2}\right)\)
P nhỏ nhất khi \(\dfrac{3}{\sqrt{x}+2}\) lớn nhất
\(\Rightarrow\sqrt{x}+2\) nhỏ nhất \(\Rightarrow\sqrt{x}+2=2\)
Khi đó: \(P_{min}=18.\left(1-\dfrac{3}{2}\right)=-9\)