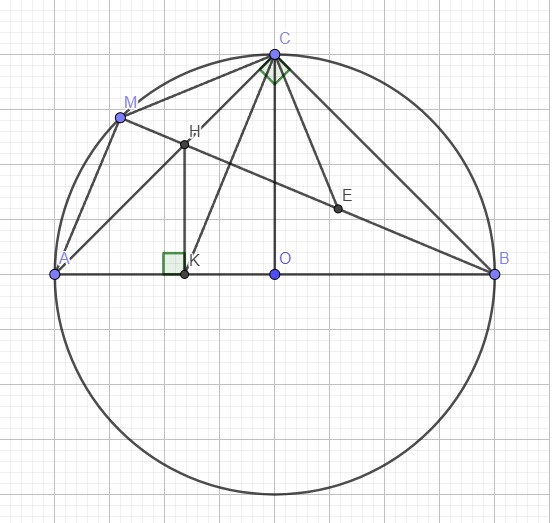
a. Em tự giải
b.
Do CBKH nội tiếp \(\Rightarrow\widehat{KCH}=\widehat{KBH}\) (cùng chắn KH)
Mà \(\widehat{KBH}=\widehat{ACM}\) (cùng chắn AM của (O))
\(\Rightarrow\widehat{ACM}=\widehat{KCH}\) hay \(\widehat{ACM}=\widehat{ACK}\)
c.
Do \(CO\perp AB\Rightarrow\widehat{COA}=\widehat{COB}=90^0\)
\(\Rightarrow sđ\stackrel\frown{AC}=sđ\stackrel\frown{BC}\Rightarrow AC=BC\)
Xét hai tam giác AMC và BEC có:
\(\left\{{}\begin{matrix}AM=BE\left(gt\right)\\\widehat{MAC}=\widehat{EBC}\left(\text{cùng chắn CM}\right)\\AC=BC\left(cmt\right)\end{matrix}\right.\)
\(\Rightarrow\Delta AMC=\Delta BEC\left(c.g.c\right)\)
\(\Rightarrow MC=EC\)
\(\Rightarrow\Delta ECM\) cân tại C (1)
Lại có \(\widehat{CME}=\widehat{CAO}=45^0\) (cùng chắn BC)
\(\Rightarrow\widehat{CEM}=\widehat{CME}=45^0\) (do \(\Delta ECM\) cân tại C)
\(\Rightarrow\widehat{MCE}=180^0-\left(\widehat{CEM}+\widehat{CME}\right)=90^0\)
\(\Rightarrow\Delta ECM\) vuông tại C (2)
(1);(2) \(\Rightarrow\Delta ECM\) vuông cân tại C