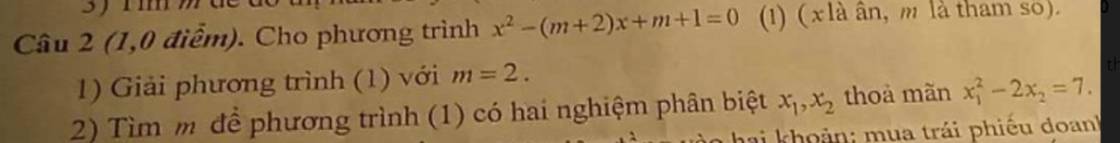1: Thay m=2 vào (1), ta được:
\(x^2-\left(2+2\right)x+2+1=0\)
=>\(x^2-4x+3=0\)
=>(x-1)(x-3)=0
=>\(\left[{}\begin{matrix}x=1\\x=3\end{matrix}\right.\)
2: \(\Delta=\left(m+2\right)^2-4\cdot1\cdot\left(m+1\right)\)
\(=m^2+4m+4-4m-4=m^2\)
Để phương trình (1) có hai nghiệm phân biệt thì m^2>0
=>\(m\ne0\)
Khi m\(\ne0\) thì phương trình có hai nghiệm phân biệt là:
\(\left[{}\begin{matrix}x=\dfrac{\left(m+2\right)-\sqrt{m^2}}{2}=\dfrac{m+2-m}{2}=\dfrac{2}{2}=1\\x=\dfrac{m+2+m}{2}=\dfrac{2m+2}{2}=m+1\end{matrix}\right.\)
\(x_1^2-2x_2=7\)
=>\(\left[{}\begin{matrix}1^2-2\left(m+1\right)=7\\\left(m+1\right)^2-2=7\end{matrix}\right.\)
=>\(\left[{}\begin{matrix}2\left(m+1\right)=-6\\\left(m+1\right)^2=9\end{matrix}\right.\)
=>\(\left[{}\begin{matrix}m+1=3\\m+1=-3\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}m=2\\m=-4\end{matrix}\right.\)