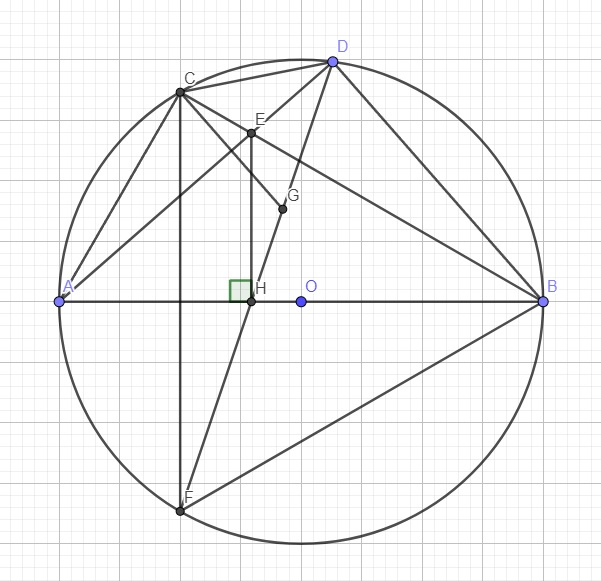
a: Xét (O) có
ΔACB nội tiếp
AB là đường kính
Do đó: ΔACB vuông tại C
Xét (O) có
ΔADB nội tiếp
AB là đường kính
Do đó: ΔADB vuông tại D
Xét tứ giác EHBD có \(\widehat{EHB}+\widehat{EDB}=90^0+90^0=180^0\)
nên EHBD là tứ giác nội tiếp
b: Xét tứ giác ACEH có \(\widehat{ECA}+\widehat{EHA}=90^0+90^0=180^0\)
nên ACEH là tứ giác nội tiếp
Xét (O) có
\(\widehat{CAD}\) là góc nội tiếp chắn cung CD
\(\widehat{CBD}\) là góc nội tiếp chắn cung CD
Do đó: \(\widehat{CAD}=\widehat{CBD}\)
mà \(\widehat{CAD}=\widehat{CHE}\)(ACEH nội tiếp)
và \(\widehat{CBD}=\widehat{EHD}\)(EHBD nội tiếp)
nên \(\widehat{CHE}=\widehat{DHE}\)
=>HE là phân giác của góc CHD
c.
Qua C kẻ đường thẳng vuông góc AB cắt (O) tại F (F khác C). Do C cố định, (O) cố định \(\Rightarrow F\) cố định
\(\Rightarrow AB\) là trung trực của CF (theo t/c đường kính vuông góc dây cung)
\(\Rightarrow BC=BF\)
Trong tam giác vuông ABC: \(cos\widehat{ACB}=\dfrac{AC}{AB}=\dfrac{R}{2R}=\dfrac{1}{2}\)
\(\Rightarrow\widehat{ACB}=60^0\Rightarrow\widehat{CBA}=90^0-60^0=30^0\)
\(\Rightarrow\widehat{CBF}=2.\widehat{CBA}=60^0\)
\(\Rightarrow\Delta BCF\) đều (tam giác cân có 1 góc vuông) \(\Rightarrow CB=CF\) (1)
Nối DF, trên DF lấy điểm G sao cho \(DC=DG\)
Ta có \(\widehat{CDF}=\widehat{CBF}=60^0\) (cùng chắn CF)
\(\Rightarrow\Delta DCG\) đều (tam giác cân có 1 góc 60 độ) \(\Rightarrow CG=CD\) (2)
Lại có \(\widehat{FCB}=\widehat{DCG}=60^0\) (các tam giác BCF, DCG đều)
\(\Rightarrow\widehat{FCB}-\widehat{BCG}=\widehat{DCG}-\widehat{BCG}\)
\(\Rightarrow\widehat{FCG}=\widehat{BCD}\) (3)
(1);(2);(3) \(\Rightarrow\Delta FCG=\Delta BCD\left(c.g.c\right)\)
\(\Rightarrow GF=BD\)
Chu vi \(ABCD=AC+AB+BD+CD=R+2R+BD+CD\)
\(=3R+BD+CD=3R+GF+DG=3R+DF\)
\(\Rightarrow\) Chu vi ABCD lớn nhất khi DF lớn nhất
\(\Rightarrow DF\) là 1 đường kính của (O)
\(\Rightarrow D\) là giao điểm của FO và (O)