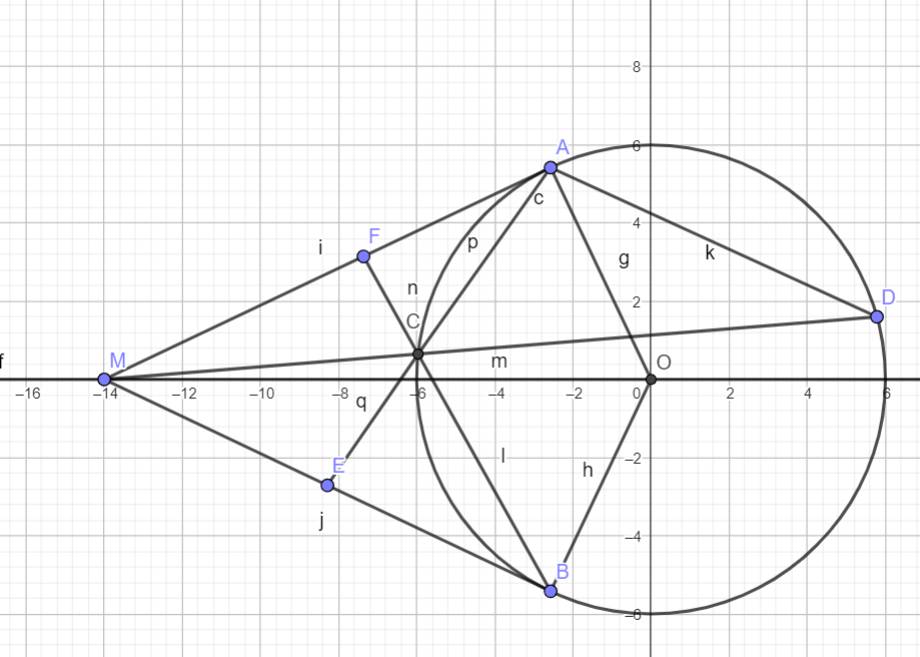
a: Xét tứ giác MAOB có \(\widehat{MAO}+\widehat{MBO}=90^0+90^0=180^0\)
nên MAOB là tứ giác nội tiếp
b: Xét (O) có
\(\widehat{EBC}\) là góc tạo bởi tiếp tuyến BE và dây cung BC
\(\widehat{BAC}\) là góc nội tiếp chắn cung BC
Do đó: \(\widehat{EBC}=\widehat{BAC}\)
Xét ΔEBC và ΔEAB có
\(\widehat{EBC}=\widehat{EAB}\)
\(\widehat{BEC}\) chung
Do đó: ΔEBC~ΔEAB
=>\(\dfrac{EB}{EA}=\dfrac{EC}{EB}\)
=>\(EB^2=EA\cdot EC\left(1\right)\)
Xét (O) có
\(\widehat{ADC}\) là góc nội tiếp chắn cung AC
\(\widehat{MAC}\) là góc tạo bởi tiếp tuyến AM và dây cung AC
Do đó: \(\widehat{ADC}=\widehat{MAC}\)
mà \(\widehat{ADC}=\widehat{EMC}\)(AD//MB)
nên \(\widehat{EMC}=\widehat{EAM}\)
Xét ΔEMC và ΔEAM có
\(\widehat{EMC}=\widehat{EAM}\)
\(\widehat{MEC}\) chung
Do đó: ΔEMC~ΔEAM
=>\(\dfrac{EM}{EA}=\dfrac{EC}{EM}\)
=>\(EM^2=EC\cdot EA\left(2\right)\)
Từ (1),(2) suy ra EB=EM
=>E là trung điểm của BM