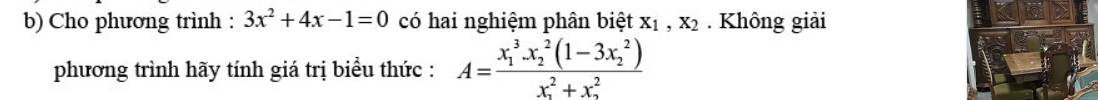Theo Vi-et, ta có:
\(\left\{{}\begin{matrix}x_1+x_2=-\dfrac{b}{a}=-\dfrac{4}{3}\\x_1x_2=\dfrac{c}{a}=-\dfrac{1}{3}\end{matrix}\right.\)
\(A=\dfrac{x_1^3\cdot x_2^2\left(1-3x_2^2\right)}{x_1^3+x_2^3}\)
\(=\dfrac{\left(x_1x_2\right)^2\cdot\left(x_1-3\cdot x_1x_2\cdot x_2\right)}{\left(x_1+x_2\right)^3-3x_1x_2\left(x_1+x_2\right)}\)
\(=\dfrac{\left(-\dfrac{1}{3}\right)^2-\left(x_1-3\cdot x_2\cdot\dfrac{-1}{3}\right)}{\left(-\dfrac{4}{3}\right)^3-3\cdot\dfrac{-1}{3}\cdot\dfrac{-4}{3}}\)
\(=\dfrac{\dfrac{1}{9}-\left(x_1+x_2\right)}{-\dfrac{100}{27}}=\dfrac{\dfrac{1}{9}-\left(-\dfrac{4}{3}\right)}{-\dfrac{100}{27}}=\left(\dfrac{1}{9}+\dfrac{4}{3}\right):\dfrac{-100}{27}\)
=-39/100