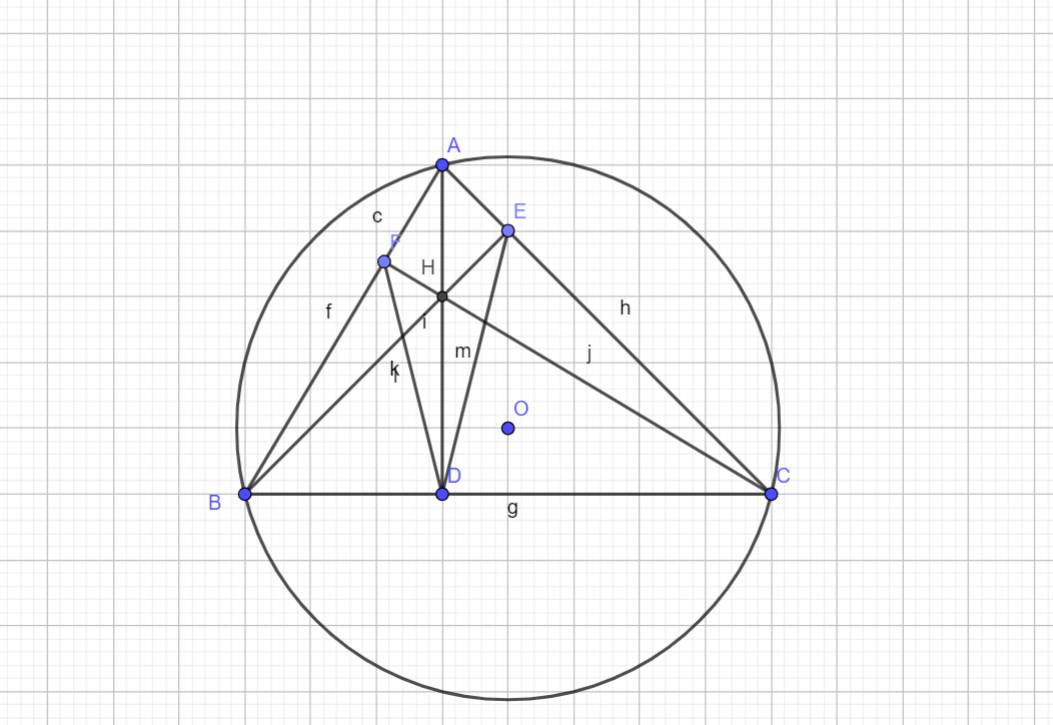
a: CF\(\perp\)AB tại F
=>\(\widehat{CFB}=90^0\)
BE\(\perp\)AC tại E
=>\(\widehat{BEC}=90^0\)
\(\widehat{BEC}+\widehat{BFC}=90^0+90^0=180^0\)
b: Ta có: \(\widehat{FCB}+\widehat{ABC}=90^0\)(ΔFBC vuông tại F)
\(\widehat{BAD}+\widehat{ABC}=90^0\)(ΔADB vuông tại D)
Do đó: \(\widehat{FCB}=\widehat{BAD}\)
c:
Gọi I là trung điểm của AH
Xét tứ giác AEHF có \(\widehat{AEH}+\widehat{AFH}=90^0+90^0=180^0\)
nên AEHF là tứ giác nội tiếp đường tròn đường kính AH
=>AEHF nội tiếp (I)
ΔFBC vuông tại F có FM là đường trung tuyến
nên MF=MC
=>ΔMFC cân tại M
=>\(\widehat{MFC}=\widehat{MCF}\)
ΔIFH cân tại I
=>\(\widehat{IFH}=\widehat{IHF}\)
mà \(\widehat{IHF}=\widehat{DHC}\)(hai góc đối đỉnh)
nên \(\widehat{IFH}=\widehat{DHC}\)
\(\widehat{IFM}=\widehat{IFC}+\widehat{MFC}=\widehat{DHC}+\widehat{DCH}=90^0\)
=>MF là tiếp tuyến của (I)