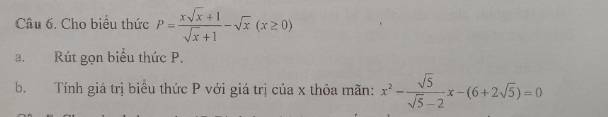a: \(P=\dfrac{x\sqrt{x}+1}{\sqrt{x}+1}-\sqrt{x}\)
\(=\dfrac{\left(\sqrt{x}+1\right)\left(x-\sqrt{x}+1\right)}{\sqrt{x}+1}-\sqrt{x}\)
\(=x-\sqrt{x}+1-\sqrt{x}=x-2\sqrt{x}+1=\left(\sqrt{x}-1\right)^2\)
b: \(x^2-\dfrac{\sqrt{5}}{\sqrt{5}-2}x-\left(6+2\sqrt{5}\right)=0\)
=>\(x^2-\sqrt{5}\left(\sqrt{5}+2\right)x-\left(6+2\sqrt{5}\right)=0\)
=>\(x^2-\left(5+2\sqrt{5}\right)x-\left(6+2\sqrt{5}\right)=0\)
=>\(x^2-\left(6+2\sqrt{5}\right)x+x-\left(6+2\sqrt{5}\right)=0\)
=>\(x\left(x-6-2\sqrt{5}\right)+\left(x-6-2\sqrt{5}\right)=0\)
=>\(\left(x-6-2\sqrt{5}\right)\left(x+1\right)=0\)
=>\(\left[{}\begin{matrix}x=6+2\sqrt{5}\left(nhận\right)\\x=-1\left(loại\right)\end{matrix}\right.\)
Thay \(x=6+2\sqrt{5}\) vào P, ta được:
\(P=\left(\sqrt{6+2\sqrt{5}}-1\right)^2\)
\(=\left(\sqrt{\left(\sqrt{5}+1\right)^2}-1\right)^2\)
\(=\left(\sqrt{5}+1-1\right)^2=5\)
= (x√x + 1 - √x(√x + 1))/(√x + 1)
= (x√x + 1 - x)/(√x + 1)
= (x√x - x + 1)/(√x + 1).Vậy, biểu thức P được rút gọn thành P = (x√x - x + 1)/(√x + 1).b. Để tính giá trị của biểu thức P với giá trị của x thỏa mãn phương trình x² - (√5/√5 - 2)x - (6 + 2√5) = 0, ta cần giải phương trình này để tìm giá trị của x.Phương trình đã cho là: x² - (√5/√5 - 2)x - (6 + 2√5) = 0.Để giải phương trình này, ta sẽ sử dụng công thức Viết.Áp dụng công thức Viết, ta có: x = (-b ± √(b² - 4ac))/(2a).Với phương trình đã cho, a = 1, b = -(√5/√5 - 2), c = -(6 + 2√5).Thay các giá trị vào công thức Viết, ta có:x = [-(√5/√5 - 2) ± √((√5/√5 - 2)² - 4(1)(-(6 + 2√5)))]/(2(1))
= [-(√5/√5 - 2) ± √((√5/√5 - 2)² + 4(6 + 2√5))]/2
= [-(√5/√5 - 2) ± √((√5/√5 - 2)² + 24 + 8√5)]/2
= [-(√5/√5 - 2) ± √((√5/√5 - 2)² + 24 + 8√5)]/2
= [-(√5/√5 - 2) ± √((√5/√5 - 2)² + 24 + 8√5)]/2.Vậy, giá trị của biểu thức P với giá trị của x thỏa mãn phương trình x² - (√5/√5 - 2)x - (6 + 2√5) = 0 là [-(√5/√5 - 2) ± √((√5/√5 - 2)² + 24 + 8√5)]/2.