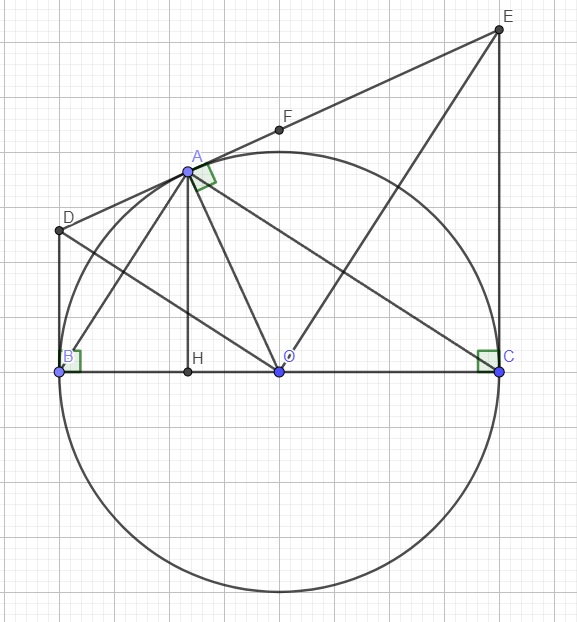
a.
Do AD là tiếp tuyến tại A \(\Rightarrow OA\perp AD\Rightarrow\widehat{OAD}=90^0\)
Do BD là tiếp tuyến tại B \(\Rightarrow\widehat{OBD}=90^0\)
\(\Rightarrow\) A và B cùng nhìn OD dưới 1 góc vuông nên tứ giác OADB nội tiếp
b.
Do D là giao điểm 2 tiếp tuyến tại A và B \(\Rightarrow\widehat{BOD}=\widehat{AOD}\)
Do E là giao điểm 2 tiếp tuyến tại A và C nên \(\widehat{AOE}=\widehat{COE}\)
\(\Rightarrow\widehat{BOD}+\widehat{AOD}+\widehat{AOE}+\widehat{COE}=2\left(\widehat{AOD}+\widehat{AOE}\right)\)
\(\Rightarrow180^0=2\widehat{DOE}\)
\(\Rightarrow\widehat{DOE}=90^0\)
c.
Do tam giác ABC vuông tại A nên O là trung điểm BC \(\Rightarrow BC=2R\)
Theo tính chất hai tiếp tuyến cắt nhau ta có: \(\left\{{}\begin{matrix}DB=AD\\CE=AE\end{matrix}\right.\)
Do \(OA\perp DE\), áp dụng hệ thức lượng trong tam giác vuông DOE với đường cao OA:
\(OA^2=AD.AE\)
\(\Leftrightarrow R^2=DB.CE\Leftrightarrow\left(2R\right)^2=4DB.CE\)
\(\Leftrightarrow BC^2=4DB.CE\)
d.
Do \(\left\{{}\begin{matrix}BD\perp BC\\EC\perp BC\end{matrix}\right.\) (t/c tiếp tuyến) \(\Rightarrow BD||EC\Rightarrow BCED\) là hình thang
Gọi F là trung điểm DE
Do tam giác DOE vuông tại O \(\Rightarrow F\) là tâm đường tròn đường kính DE và \(OF\) là 1 bán kính (1)
O là trung điểm BC, F là trung điểm DE \(\Rightarrow OF\) là đường trung bình hình thang BCED
\(\Rightarrow OF||BD\)
Mà \(BD\perp BC\Rightarrow OF\perp BC\) (2)
(1);(2) \(\Rightarrow BC\) là tiếp tuyến của đường tròn đường kính DE