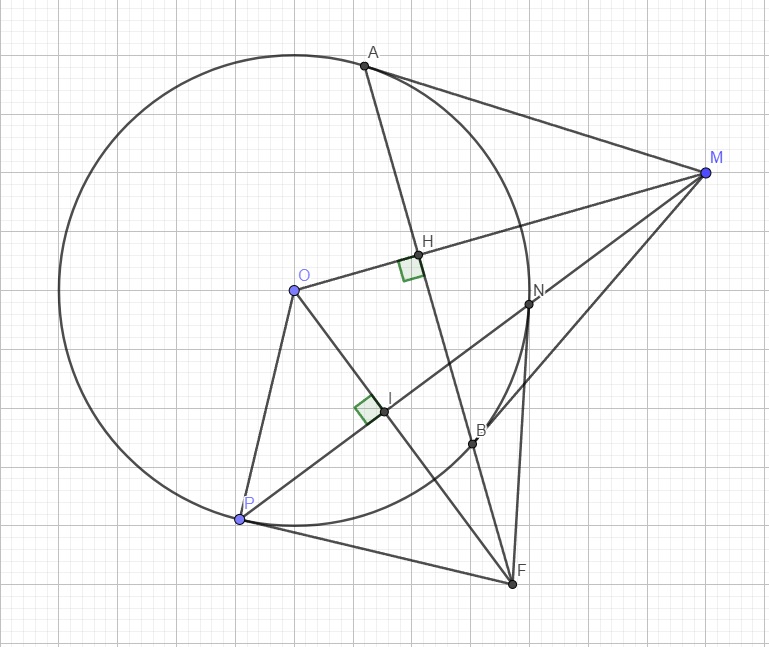
a: Ta có: ΔONP cân tại O
mà OI là đường trung tuyến
nên OI\(\perp\)NP
Ta có: \(\widehat{OIM}=\widehat{OAM}=90^0\)
=>O,I,M,A cùng thuộc đường tròn đường kính OM
b: Xét (O) có
MA,MB là các tiếp tuyến
Do đó: MA=MB
=>M nằm trên đường trung trực của AB(1)
ta có: OA=OB
=>O nằm trên đường trung trực của AB(2)
Từ (1),(2) suy ra OM là đường trung trực của AB
=>OM\(\perp\)AB tại H
Xét ΔOAM vuông tại A có AH là đường cao
nên \(OH\cdot OM=OA^2=R^2\) không đổi
c.
Ta có: \(\left\{{}\begin{matrix}ON=OP=R\\FN=FP\left(\text{t/c hai tiếp tuyến cắt nhau}\right)\end{matrix}\right.\)
\(\Rightarrow OF\) là trung trực NP
\(\Rightarrow OF\) vuông góc NP tại I
Do PF là tiếp tuyến \(\Rightarrow PF\perp OP\)
Áp dụng hệ thức lượng trong tam giác vuông OPF với đường cao PI:
\(OP^2=OI.OF\Rightarrow R^2=OI.OF\)
\(\Rightarrow OI.OF=OH.OM\) (từ kết quả câu b)
\(\Rightarrow\dfrac{OI}{OH}=\dfrac{OM}{OF}\)
Xét hai tam giác IOM và HOF có:
\(\left\{{}\begin{matrix}\dfrac{OI}{OH}=\dfrac{OM}{OF}\left(cmt\right)\\\widehat{IOH}\text{ chung}\end{matrix}\right.\) \(\Rightarrow\Delta IOM\sim\Delta HOF\left(c.g.c\right)\)
\(\Rightarrow\widehat{OHF}=\widehat{OIM}=90^0\)
Hay \(FH\perp OH\)
Mà \(AH\perp OH\)
\(\Rightarrow F,A,H\) thẳng hàng
Hay F luôn nằm trên đường thẳng AB cố định khi d quay quanh M