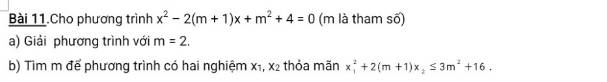a. Em tự giải
b.
\(\Delta'=\left(m+1\right)^2-\left(m^2+4\right)=2m-3\)
Pt có 2 nghiệm khi \(2m-3\ge0\Rightarrow m\ge\dfrac{3}{2}\)
Theo hệ thức Viet: \(\left\{{}\begin{matrix}x_1+x_2=2\left(m+1\right)\\x_1x_2=m^2+4\end{matrix}\right.\)
Do \(x_1\) là nghiệm nên:
\(x_1^2-2\left(m+1\right)x_1+m^2+4=0\Rightarrow x_1^2=2\left(m+1\right)x_1-m^2-4\)
Thay vào:
\(2\left(m+1\right)x_1-m^2-4+2\left(m+1\right)x_2\le3m^2+16\)
\(\Leftrightarrow2\left(m+1\right)\left(x_1+x_2\right)\le4m^2+20\)
\(\Leftrightarrow4\left(m+1\right)^2\le4m^2+20\)
\(\Leftrightarrow2m\le4\)
\(\Rightarrow m\le2\)
Kết hợp điều kiện delta \(\Rightarrow\dfrac{3}{2}\le m\le2\)
a: Thay m=2 vào phương trình, ta được:
\(x^2-2\left(2+1\right)x+2^2+4=0\)
=>\(x^2-6x+8=0\)
=>\(\left(x-2\right)\left(x-4\right)=0\)
=>\(\left[{}\begin{matrix}x-2=0\\x-4=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=2\\x=4\end{matrix}\right.\)
b: \(\text{Δ}=\left[-2\left(m+1\right)\right]^2-4\cdot1\cdot\left(m^2+4\right)\)
\(=\left(2m+2\right)^2-4m^2-16\)
\(=4m^2+8m+4-4m^2-16=8m-12\)
Để phương trình có hai nghiệm thì Δ>=0
=>8m-12>=0
=>8m>=12
=>\(m>=\dfrac{3}{2}\)(1)
Theo Vi-et, ta có:
\(\left\{{}\begin{matrix}x_1+x_2=-\dfrac{b}{a}=\dfrac{-\left[-2\left(m+1\right)\right]}{1}=2\left(m+1\right)\\x_1\cdot x_2=\dfrac{c}{a}=\dfrac{m^2+4}{1}=m^2+4\end{matrix}\right.\)
\(x_1^2+2\left(m+1\right)x_2< =3m^2+16\)
=>\(x_1^2+x_2\left(x_1+x_2\right)< =3m^2+16\)
=>\(x_1^2+x_2^2+x_1x_2< =3m^2+16\)
=>\(\left(x_1+x_2\right)^2-x_1x_2< =3m^2+16\)
=>\(\left(2m+2\right)^2-m^2-4< =3m^2+16\)
=>\(4m^2+8m+4-m^2-4-3m^2-16< =0\)
=>\(8m-16< =0\)
=>8m<=16
=>m<=2(2)
Từ (1),(2) suy ra \(\dfrac{3}{2}< =m< =2\)