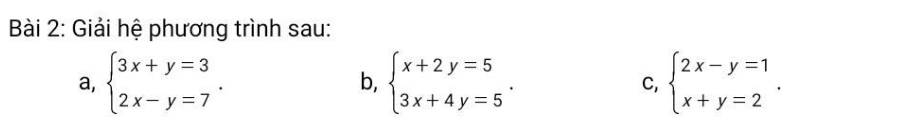a: \(\left\{{}\begin{matrix}3x+y=3\\2x-y=7\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}3x+y+2x-y=3+7\\2x-y=7\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}5x=10\\2x-y=7\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=2\\y=2x-7=2\cdot2-7=-3\end{matrix}\right.\)
b: \(\left\{{}\begin{matrix}x+2y=5\\3x+4y=5\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}2x+4y=10\\3x+4y=5\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}2x+4y-3x-4y=10-5\\x+2y=5\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}-x=5\\2y=5-x\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=-5\\2y=5-\left(-5\right)=10\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x=-5\\y=5\end{matrix}\right.\)
c: \(\left\{{}\begin{matrix}2x-y=1\\x+y=2\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}2x-y+x+y=1+2\\x+y=2\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}3x=3\\x+y=2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=1\\y=2-x=2-1=1\end{matrix}\right.\)
\(a,\\ \left\{{}\begin{matrix}3x+y=3\\2x-y=7\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}5x=10\\2x-y=7\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=2\\2.2-y=7\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=2\\y=-3\end{matrix}\right.\\ Vậy:\left(x;y\right)=\left(2;-3\right)\\ ---\\ b,\\ \left\{{}\begin{matrix}x+2y=5\\3x+4y=5\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}3x+6y=15\\3x+4y=5\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}2y=10\\x+2y=5\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=5\\x+2.5=5\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=5\\x=-5\end{matrix}\right.\\ Vậy:\left(x;y\right)=\left(-5;5\right)\\ ---\\ c,\\ \left\{{}\begin{matrix}2x-y=1\\x+y=2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}3x=3\\x+y=2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=1\\1+y=2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=1\\y=1\end{matrix}\right.\\ Vậy:\left(x;y\right)=\left(1;1\right)\)