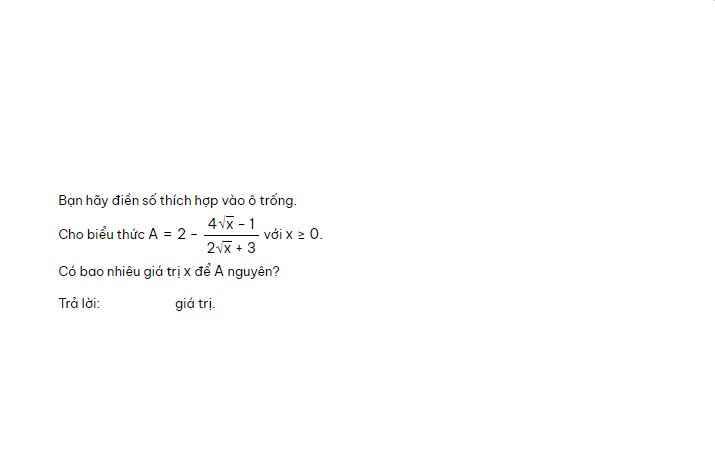ĐKXĐ: x>=0
\(A=2-\dfrac{4\sqrt{x}-1}{2\sqrt{x}+3}\)
\(=\dfrac{2\left(2\sqrt{x}+3\right)-4\sqrt{x}+1}{2\sqrt{x}+3}\)
\(=\dfrac{4\sqrt{x}+6-4\sqrt{x}+1}{2\sqrt{x}+3}=\dfrac{7}{2\sqrt{x}+3}\)
Để A là số nguyên thì \(7⋮2\sqrt{x}+3\)
=>\(2\sqrt{x}+3\inƯ\left(7\right)\)
=>\(2\sqrt{x}+3\in\left\{1;-1;7;-7\right\}\)
mà \(2\sqrt{x}+3>=3\forall x\) thỏa mãn ĐKXĐ
nên \(2\sqrt{x}+3=7\)
=>\(2\sqrt{x}=4\)
=>\(\sqrt{x}=2\)
=>x=4
=>Có 1 giá trị nguyên của x thỏa mãn A nguyên
\(A=2-\dfrac{4\sqrt{x}-1}{2\sqrt{x}+3}\left(x\ge0\right)\)
\(=\dfrac{2\left(2\sqrt{x}+3\right)}{2\sqrt{x}+3}-\dfrac{4\sqrt{x}-1}{2\sqrt{x}+3}\)
\(=\dfrac{4\sqrt{x}+6-4\sqrt{x}+1}{2\sqrt{x}+3}\)
\(=\dfrac{7}{2\sqrt{x}+3}\)
Để \(A\) nguyên thì \(\dfrac{7}{2\sqrt{x}+3}\) nhận giá trị nguyên
\(\Rightarrow7⋮2\sqrt{x}+3\)
\(\Rightarrow2\sqrt{x}+3\inƯ\left(7\right)\)
\(\Rightarrow2\sqrt{x}+3\in\left\{1;7;-1;-7\right\}\)
\(\Rightarrow2\sqrt{x}\in\left\{-2;4;-4;-10\right\}\) mà \(2\sqrt{x}\ge0\forall x\ge0\)
\(\Rightarrow2\sqrt{x}=4\)
\(\Rightarrow\sqrt{x}=2\)
\(\Rightarrow x=4\left(tm\right)\)
\(\Rightarrow\) Có 1 giá trị của \(x\) thoả mãn \(A\) nguyên.