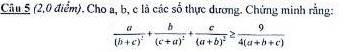Chúng ta sẽ giả sử a+b+c=3 để không làm mất tính tổng quát
Vì a+b+c=3 và a,b,c dương
nên \(a,b,c\in(0;3]\)
Giả sử \(\dfrac{a}{\left(3-a\right)^2}>=\dfrac{2a-1}{4}\)
=>\(\dfrac{a}{\left(3-a\right)^2}-\dfrac{2a-1}{4}>=0\)
=>\(\dfrac{\left(a+1\right)^2\left(9-2a\right)}{4\left(3-a\right)^2}>=0\)
\(a\in(0;3]\)
=>\(-2a\in[-6;0)\)
=>\(-2a+9\in[3;9)\)
=>-2a+9>0 với mọi a thuộc (0;3]
mà \(\left\{{}\begin{matrix}\left(a+1\right)^2>=0\\4\left(3-a\right)^2>=0\end{matrix}\right.\forall a\in(0;3]\)
nên \(\dfrac{\left(a+1\right)^2\left(9-2a\right)}{4\left(3-a\right)^2}>=0\forall a\in(0;3]\)
=>\(\dfrac{a}{\left(3-a\right)^2}>=\dfrac{2a-1}{4}\)
Chứng minh tương tự, ta được: \(\dfrac{b}{\left(3-b\right)^2}>=\dfrac{2b-1}{4};\dfrac{c}{\left(3-c\right)^2}>=\dfrac{2c-1}{4}\)
=>\(\dfrac{a}{\left(3-a\right)^2}+\dfrac{b}{\left(3-b\right)^2}+\dfrac{c}{\left(3-c\right)^2}>=\dfrac{2a-1+2b-1+2c-1}{4}=\dfrac{2\cdot3-3}{4}=\dfrac{3}{4}\)
=>\(\dfrac{a}{\left(b+c\right)^2}+\dfrac{b}{\left(c+a\right)^2}+\dfrac{c}{\left(a+b\right)^2}>=\dfrac{9}{4\left(a+b+c\right)}\)
\(a,b,c>0\)
\(\sum\dfrac{a}{\left(b+c\right)^2}\ge\dfrac{9}{4\left(a+b+c\right)}\)
\(\Leftrightarrow\sum\dfrac{a\left(a+b+c\right)}{\left(b+c\right)^2}\ge\dfrac{9}{4}\)
\(\Leftrightarrow\sum\left(\dfrac{a}{b+c}\right)^2+\sum\left(\dfrac{a}{b+c}\right)\ge\dfrac{9}{4}\)
Ta sẽ chứng minh \(\sum\dfrac{a}{b+c}\ge\dfrac{3}{2}\) (note: đây là BDT Nesbitt và có rất nhiều cách chứng minh BDT này, sau đây anh sử dụng BDT Cauchy-Schwarz).
Thật vậy, áp dụng BDT Cauchy-Schwarz (dạng phân thức), ta có:
\(\sum\dfrac{a}{b+c}=\sum\dfrac{a^2}{ab+ac}\ge\dfrac{\left(a+b+c\right)^2}{2\left(ab+bc+ca\right)}\ge\dfrac{3\left(ab+bc+ca\right)}{2\left(ab+bc+ca\right)}=\dfrac{3}{2}\left(1\right)\)
Từ đây ta cũng có:
\(\sum\left(\dfrac{a}{b+c}\right)^2\ge\dfrac{\left(\sum\dfrac{a}{b+c}\right)^2}{3}\ge\dfrac{\left(\dfrac{3}{2}\right)^2}{3}=\dfrac{3}{4}\left(2\right)\)
Lấy (1)+(2) ta được bất đẳng thức ban đầu. Vậy ta có điều phải chứng minh.
Dấu "=" xảy ra khi \(a=b=c\)