2)

\(\Delta ABC\) vuông tại A
\(\Rightarrow BC^2=AB^2+AC^2\left(Pytago\right)\)
\(=2^2+\left(2\sqrt{3}\right)^2\)
\(=16\)
\(\Rightarrow BC=4\left(cm\right)\)
Ta có:
\(AH.BC=AB.AC\Rightarrow AH=\dfrac{AB.AC}{BC}=\dfrac{2.2\sqrt{3}}{4}=\sqrt{3}\left(cm\right)\)
\(sinB=\dfrac{AC}{BC}=\dfrac{2\sqrt{3}}{4}=\dfrac{\sqrt{3}}{2}\)
\(\Rightarrow\widehat{B}=60^0\)
1:
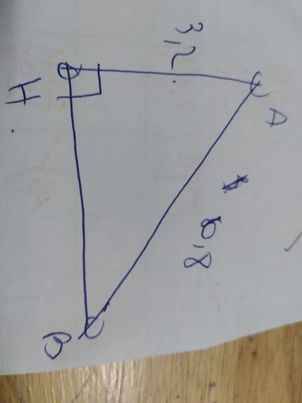
Gọi AH là độ cao kẻ từ A xuống mặt đất
=>AH vuông góc HB tại H
Theo đề, ta có: AH=3,2km và AB=6,8km
Xét ΔAHB vuông tại H có
\(sinABH=\dfrac{AH}{AB}=\dfrac{3.2}{6,8}=\dfrac{8}{17}\)
=>\(\widehat{ABH}\simeq28^0\)
Bài IV
1)

\(\Delta ABC\) vuông tại C
\(\Rightarrow sinB=\dfrac{AC}{BC}=\dfrac{3,2}{6,8}=\dfrac{8}{17}\)
\(\Rightarrow\widehat{B}\simeq28^0\)
Vậy góc nhọn tạo bởi đường bay AB và phương ngang của mặt đất là \(28^0\)
















